Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\frac{5a-17}{4a-23}=\frac{\frac{5}{4}x\left(4a-23\right)+\frac{115}{4}-17}{4a-23}=\frac{5}{4}+\frac{47}{4x\left(4a-23\right)}\)
Để \(A\) lớn nhất thì \(\frac{1}{4a-23}\) là số dương lớn nhất => 4a - 23 là nhỏ nhất mà \(A\) là số tự nhiên => 4a - 23 = 1 => \(A\) = 6
Vậy \(A\) = 6 thì \(A\) lớn nhất bằng \(\frac{5}{4}+\frac{47}{4}=\frac{52}{4}=13\)
Có được GP không vậy ?

Ta có :
\(\frac{20a+13}{4a+3}=\frac{20a+15}{4a+3}-\frac{2}{4a+3}=5-\frac{2}{4a+3}\) đạt GTNN
<=> \(\frac{2}{4a+3}\) đạt GTLN <=> 4a + 3 đạt GTNN
Xét 4a + 3 > 0 vì nếu 4a + 3 < 0 thì \(\frac{2}{4a+3}<0\) do đó không thể đạt GTLN
Mà 4a + 3 > 0 đạt GTNN <=> 4a > 0 đạt GTNN <=> 4a = 0 <=> a = 0
Vậy a = 0

Để \(\frac{20+13}{4a+3}=\frac{33}{4a+3}\) đạt giá trị nhỏ nhất thì 4a+3 đạt giá trị nhỏ nhất và \(33\left(4a+3\right)\ge0\)
\(\Rightarrow4a\) đạt giá trị nhỏ nhất là số nguyên dương
\(\Rightarrow a=0\)
A=\(\frac{4n+3}{2n+1}\) B=\(\frac{6n+2}{n+1}\)
tìm các số tự nhiên n để các phân số trên là tối giản


y ' = 4 x 3 - 4 m 2 + 1 x y ' = 0 ⇔ x = 0 x = ± m 2 + 1
Dễ thấy hàm số đã cho có 3 điểm cực trị với mọi m.
Với x C T = ± m 2 + 1 ⇒ giá trị cực tiểu y C T = - m 2 + 1 + 1
Ta có m 2 + 1 2 ≥ 1 ⇒ y C T ≤ 0 m a x y C T = 0 ⇔ m 2 + 1 = 1 ⇔ m = 0
Đáp án A

Đáp án B
Ta có y ' = 4 x 3 - 4 m 2 + 1 x , ∀ x ∈ ℝ . Phương trình y ' = 0 ⇔ [ x = 0 x = m 2 + 1 .
Hệ số a > 0 suy ra giá trị cực tiểu của hàm số là y C T = 2 - m 2 + 1 4 ≤ 1
Dấu “=” xảy ra khi và chỉ khi m 2 = 0 ⇒ m = 0 .

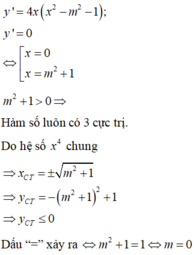
\(M=\frac{6n-3}{4n-6}=\frac{6n-9+6}{4n-6}=\frac{3\left(2n-3\right)}{2\left(2n-3\right)}+\frac{6}{4n-6}=\frac{3}{2}+\frac{6}{4n-6}\)
Do đó, để M có giá trị lớn nhất thì 6/(4n-6) có giá trị lớn nhất
=>4n-6 có giá trị nhỏ nhất(nEN)
=>4n-6=2
4n=6+2
4n=8
n=8/4=2
Nếu n=2 thì M=\(\frac{3}{2}+\frac{6}{4\cdot2-6}=\frac{3}{2}+\frac{6}{8-6}=\frac{3}{2}+3=\frac{3}{2}+\frac{6}{2}=\frac{9}{2}=4,5\)
Vậy M đạt giá trị lớn nhất là 4,5 tại n=2