Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\dfrac{5-n}{7+n}=\dfrac{1}{3}\)
\(\Leftrightarrow3\left(7+n\right)=5-n\)
\(\Leftrightarrow3n+21-5+n=0\)
\(\Leftrightarrow4n+16=0\)
\(\Leftrightarrow4n=-16\)
hay n=-4
Vậy: n=-4
b) Ta có: \(\dfrac{3+n}{18-n}=\dfrac{3}{4}\)
\(\Leftrightarrow4\left(n+3\right)=3\left(18-n\right)\)
\(\Leftrightarrow4n+12-54+3n=0\)
\(\Leftrightarrow7n=42\)
hay n=6
Vậy: n=6

Theo đầu bài ta có:
\(\frac{a+71}{b}=\frac{18}{11}\)
\(\Rightarrow11\left(a+71\right)=18b\)
\(\Rightarrow11a+781=18b\)
Chú ý rằng do a/b = 5/7 nên a = 5k còn b = 7k ( với k thuộc N ). Từ đó suy ra:
\(\Rightarrow11\cdot5k+781=18\cdot7k\)
\(\Rightarrow55k+781=126k\)
\(\Rightarrow71k=781\)
\(\Rightarrow k=11\)
\(\Rightarrow\frac{a}{b}=\frac{5k}{7k}=\frac{5\cdot11}{7\cdot11}=\frac{55}{77}\)

1) Khi bớt ở cả tử số và mẫu số của một phân số thì hiệu giữa mẫu số và tử số của phân số đó không thay đổi. Vậy hiệu giữa mẫu số và tử số là:
47 - 23 = 24
Coi tử số mới là 7 phần bằng nhau thì mẫu số mới là 13 phần như thế, hiệu là 24.
Hiệu số phần bằng nhau là:
13 - 7 = 6 (phần)
Giá trị 1 phần là:
24 : 6 = 4
Tử số mới là:
4 . 7 = 28
Số nguyên cần tìm là:
23 - 28 = -5
Đáp số: -5
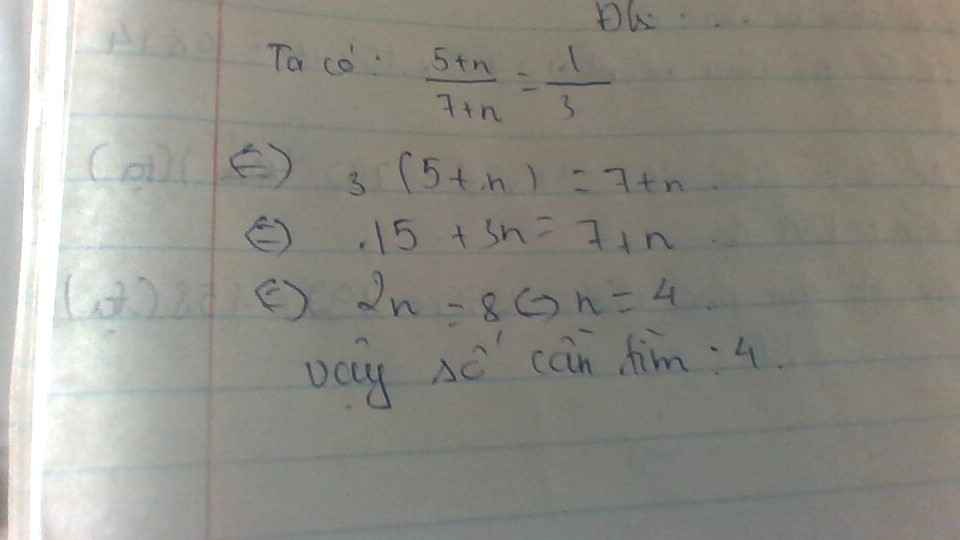
Đáp án:
45/105
Giải thích các bước giải:
Theo bài ra ta có : \(\frac{a}{b}=\frac{3}{7}\)
hay :\(\frac{a}{25+b}\)
nếu coi b là 21 phần bằng nhau thì a+25 là 14 phần bằng nhau như thế và a là 9 phần bằng nhau như thế.
suy ra 25 chính là : 14-9 = 5 (phần )
a là : 25:5 x 9=45
b là : 25:5 x 21 =105
vậy phân số đó là \(\frac{45}{105}\)
Theo bài ra ta có : a/b = 3/7
hay :a+25/b
nếu coi b là 21 phần bằng nhau thì a+25 là 14 phần bằng nhau như thế và a là 9 phần bằng nhau như thế.
suy ra 25 chính là : 14-9 = 5 (phần )
a là : 25 : 5 x 9=45
b là : 25 : 5 x 21 =105
vậy phân số đó là 45/105