Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

T/C của gttđ là >= 0 nên
a) GTNN = -4
b) GTLN = 2
c) GTNN = 2

\(A=\left|x-102\right|+\left|2-x\right|\ge\left|x-102+2-x\right|=100\)
Dấu "=" xảy ra <=> \(\left(x-102\right)\left(2-x\right)\ge0\)
Xét 2 trường hợp:
\(\hept{\begin{cases}x-102\ge0\\2-x\ge0\end{cases}}\) Hoặc \(\hept{\begin{cases}x-102\le0\\2-x\le0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge102\\x\le2\end{cases}}\) (Loại) Hoặc \(\hept{\begin{cases}x\le102\\x\ge2\end{cases}}\) (Nhận)
\(\Leftrightarrow2\le x\le102\)
Vậy AMin = 100 khi và chỉ khi \(2\le x\le102\)

a) \(A=2x^2+1\)
Vì \(x^2\ge0\)\(\forall x\)\(\Rightarrow2x^2\ge0\)\(\forall x\)
\(\Rightarrow2x^2+1\ge1\)\(\forall x\)
hay \(A\ge1\)
Dấu " = " xảy ra \(\Leftrightarrow x=0\)
Vậy \(minA=1\)\(\Leftrightarrow x=0\)
b) \(B=-3x^2-1\)
Vì \(x^2\ge0\forall x\)\(\Rightarrow-3x^2\le0\forall x\)
\(\Rightarrow-3x^2-1\le-1\forall x\)
hay \(B\le-1\)
Dấu " = " xảy ra \(\Leftrightarrow x=0\)
Vậy \(maxB=-1\Leftrightarrow x=0\)
c) Ta có: \(C=\left|-3x^2\right|\ge0\)( tính chất của dấu giá trị tuyệt đối )
Dấu " = " xảy ra \(\Leftrightarrow-3x^2=0\)\(\Leftrightarrow x=0\)
Vậy \(minC=0\Leftrightarrow x=0\)

Với mọi x ta có :
\(\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|+5\ge0\)
\(\Leftrightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy..
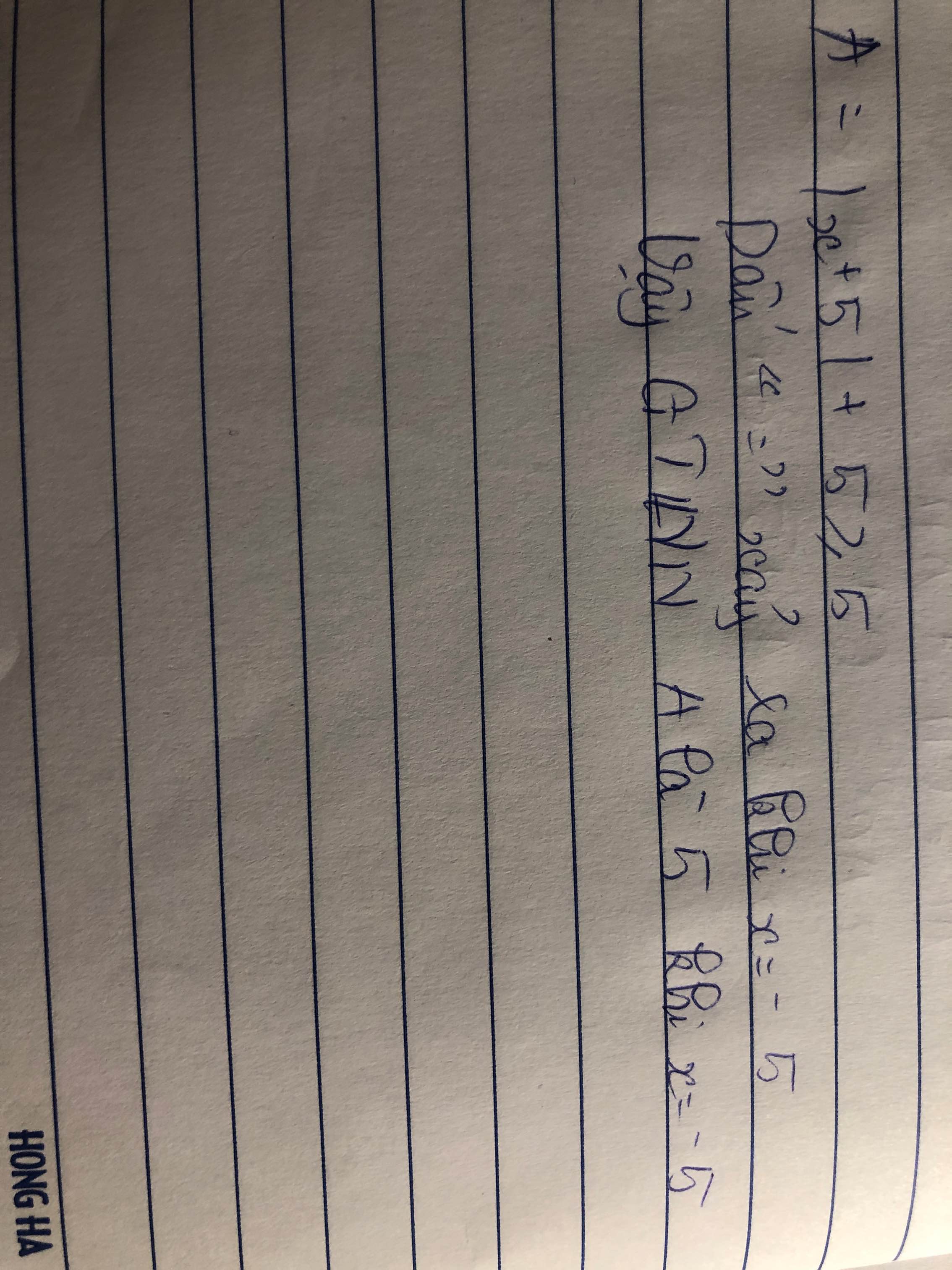
\(\left|x+1,5\right|\ge0\forall x\)
Dấu " = " xảy ra khi
| x + 1,5 | = 0
x = -1,5
Vậy MinA = 0 <=> x = -1,5
b)
\(\left|x-2\right|\ge0\forall x\Rightarrow\left|x-2\right|-\frac{9}{10}\ge\frac{9}{10}\forall x\)
Dấu " = " xảy ra khi
| x - 2 | = 0
x = 2
Vậy MinA = \(\frac{9}{10}\)<=> x = 2
\(-\left|2x-1\right|\le0\forall x\)
Dấu " = " xảy ra khi :
- | 2x - 1 | = 0
=> x = \(\frac{1}{2}\)
Vậy MaxA = 0 <=> x = \(\frac{1}{2}\)
b)
\(-\left|5x-3\right|\le0\forall x\Rightarrow4-\left|5x-3\right|\le4\)
Dấu " = " xảy ra khi :
- | 5x - 3 | = 0
=> x = \(\frac{3}{5}\)
Vậy MaxB = 4 <=> x = \(\frac{3}{5}\)
Study well