NT
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
3
26 tháng 4 2016
A=(x+1)*(x+2)*(x+3)*(x+4)
Ta có (x+1);(x+2);(x+3) và (x+4) sẽ xảy ra các trường hợp sau
Th1:(x+1);(x+2);(x+3) và (x+4) đều là số âm
Nên tích (x+1)*(x+2)*(x+3)*(x+4) sẽ là số dương
Hay (x+1)*(x+2)*(x+3)*(x+4)>0
Th2:1 trong các số (x+1);(x+2);(x+3);(x+4) sẽ=0
Nên (x+1)*(x+2)*(x+3)*(x+4)=0
Th2:các số (x+1);(x+2);(x+3);(x+4) đều là số dương
Nên (x+1)*(x+2)*(x+3)*(x+4)>0
Trong các trường hợp trên thì ta thấy trường hợp có GTNN là th2 nên biểu thức A sẽ có giá trị nhỏ nhất là 0(tick nha)
BH
4
BH
1
HT
24 tháng 3 2016
Có |x+4| \(\ge\) với mọi x (Định nghĩa giá trị tuyệt đối)
Suy ra B=|x+4|+1996 \(\ge\) 1996 với mọi x
Dấu "=" xảy ra \(\Leftrightarrow\) |x+4| = 0 \(\Leftrightarrow\) x+4 = 0 \(\Leftrightarrow\) x = -4
Vậy \(B_{m\text{ax}}=1996\) tại x = -4
BH
1
23 tháng 3 2016
Ta có:
\(D=\frac{x+5}{x-4}=\frac{\left(x-4\right)+9}{x-4}=\frac{x-4}{x-4}+\frac{9}{x-4}=1+\frac{9}{x-4}\)
ĐểD đạt giá trị nhỏ nhất thì \(\frac{9}{x-4}\) đạt giá trị nhỏ nhất
\(\Rightarrow x-4\) phải đạt giá trị lớn nhất là âm
\(\Rightarrow x-4=-1\)
\(\Rightarrow x=3\)
\(D=1+\frac{9}{-1}=-8\)
Vậy để biểu thức đạt giá trị nhỏ nhất là -8 thì x=3
CM
29 tháng 3 2018
ĐK:
Ta có
log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4
Xét hàm số f ( x ) = log 3 t + 3 t t > 0
có f ' ( t ) = 1 t ln 3 + 3 > 0 ; ∀ t > 0 nên hàm số đồng biến trên 0 ; + ∞
Kết hợp (*) suy ra
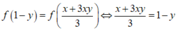
Xét P = x + y ⇒ x = P - y thay vào (**) ta được
Ta tìm giá trị nhỏ nhất của g ( y ) = 3 y 2 - 2 y + 3 3 y + 1 trên (0;1)
Ta có
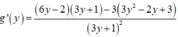
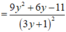
Giải phương trình
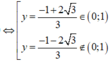
Lại có g ' ( y ) < 0 ∀ y ∈ 0 ; - 1 + 2 3 3
và g ' ( y ) > 0 ∀ y ∈ - 1 + 2 3 3 ; 1
Hay g'(y) đổi dấu từ âm sang dương tại y = - 1 + 2 3 3 nên
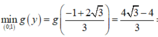
⇒ P m i n = 4 3 - 4 3
Chọn đáp án A.
CM
27 tháng 6 2017
Đáp án C
Đặt t = y x > 1 ⇒ y = t x ⇒ P = log x t x 2 - 1 2 + 8 log t t x x 2
= log x t 2 + 1 2 + 8 log t t x - log t x 2 = 2 log x t 2 + 1 2 + 8 1 + log t x - 1 2 log t x 2
Đặt u = log t x ⇒ P = 2 u + 1 2 + 8 1 + 1 2 u 2 = 4 u 2 + 4 u + 2 u 2 + 8 u + 9 = P u
Do u = log x y x = log x y - 1 > 0 nên xét P u u > 0 ⇒ P ' u = 8 u + 4 - 4 u 3 - 8 u 2
= 4 2 u + 1 u 3 - 1 u 3 = 0 → u > 0 u = 1 . Do đó ta tìm được P m i n = P 1 = 27 .
CM
4 tháng 2 2019
Đáp án A
Xét hệ phương trình
f ' ( x ) = 3 x 2 + 6 a x + 3 = 0 ( * ) g ' ( x ) = 3 x 2 + 6 b x + 9 = 0 ⇒ 6 x ( a − b ) = 6 ⇔ x = 1 a − b .
Áp dụng công thức nghiệm do phương trình (*) ta có x = − a ± a 2 − 1 với a ∈ ( − ∞ ; − 1 ) ∪ 1 ; + ∞ .
*Trường hợp 1: x = − a + a 2 − 1 .
Ta có
1 a − b = − a + a 2 − 1 ⇔ b = a + 1 a − a 2 − 1 = 2 a + a 2 − 1
Suy ra
P = a + 2 b = a + 4 a + 2 a 2 − 1 ≥ 5 a + 2 a 2 − 1
Xét hàm số
f ( x ) = 5 x + 2 x 2 − 1 ; x ∈ − ∞ ; − 1 ∪ 1 ; + ∞ .
Đạo hàm
f ' x = 5 + 2 x x 2 − 1 ; f ' x = 0 ⇔ 5 x 2 − 1 = − 2 x ⇔ x ≤ 0 25 x 2 − 1 = 4 x 2
⇔ x = − 5 21 (thỏa mãn).
Lại có f − 5 21 = − 21 ⇒ P ≥ 21 (lập bảng biến thiên của hàm số f x ).
*Trường hợp 2:Tương tự, ta tìm được P ≥ 21 .
Ta có : H = |x - 3| - |4 + x| \(\ge\left|x-3-4-x\right|=-7\)
Vậy GTNN của biểu thức là -7
hc3,,a x x