Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt A=(n^4-3n^3+n^2-3n+10)/(n^2+1)
=(n^4+n^2-3n^3-3n+1)/(n^2+1)
=[n^2(n^2+1)-3n(n^2+1)+1]/(n^2+1)
=[(n^2+1)(n^2-3n)+1]/(n^2+1)
để A E Z thì tử phải chia hết cho mẫu,mà (n^2+1)(n^2-3n) chia hết cho (n^2+1)
=>1 chia hết cho n^2+1
=>n^2+1 E Ư(1)
mà n^2+1 >= 1 (với mọi n)
=>n^2+1 chỉ có thể = 1
=>n=0
Vậy...............
Ta có (n^4-3n^3+n^2-3n+10)/(n^2+1)
= (n^4+n^2-3n^3-3n+1)/(n^2+1)
= [n^2(n^2+1)-3n(n^2+1)+1]/(n^2+1)
[(n^2+1)(n^2-3n)+1]/(n^2+1)
Để biểu thức nguyên
<=> [(n^2+1)(n^2-3n)+1] chia hết cho n^2+1
mà 1 chia hết cho n^2+1
n^2+1 thuộc Ư(1)
XÉT n^2+1=1
n =0
xát n^2+1 =-1( vô lí)
Vậy n = 0 thì bt nguyên

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

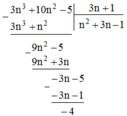
Ta có: 3 n 3 + 10 n 2 - 5 = 3 n + 1 n 2 + 3 n - 1 - 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n = 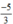 ∉ Z : loại
∉ Z : loại
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n = 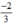 ∉ Z : loại
∉ Z : loại
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n = 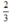 ∉ Z : loại
∉ Z : loại
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì 3 n 3 + 10 n 2 - 5 chia hết cho 3n + 1.

a) Cho x2 - x + 5=0 =>x={ \(\frac{1}{2}+\frac{\sqrt{19}}{2}i;\frac{1}{2}-\frac{\sqrt{19}}{2}i\) }
Thay giá trị của x là \(\frac{1}{2}+\frac{\sqrt{19}}{2}i\)hoặc \(\frac{1}{2}-\frac{\sqrt{19}}{2}i\) vừa tìm được vào x4 - x3 + 6x2- x sẽ luôn được kết quả là -5
=>-5 +a=0 => a=5
b) Cho x+2=0 => x=-2
Thay giá trị của x vào biểu thức 2x3 - 3x2 + x sẽ được kết quả là -30
=> -30 + a=0 => a=30
a) Cho 3n +1 =0 => n= \(\frac{-1}{3}\)
Thay n= \(\frac{-1}{3}\)vào biểu thức 3n3 + 10n2 -5 sẽ được kết quả -4
Vậy n = -4
b) Cho n-1=0 => n=1
Thay n=1 vào biểu thức 10n2 + n -10 sẽ được kết quả là 1
Vậy n = 1

a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
n^4 - 3x^3 + n^2 - 3n + 1 n^2 + 1 n^2 - 3n n^4 + n^2 - 3n^3 - 3n + 1 - 3n^3 -3n 1
Để chia \(n^4-3n^3+n^2-3n+1\) cho \(n^2+1\) có giá trị nguyên
⇔ \(n^4-3n^3+n^2-3n+1\) \(⋮n^2+1\)
⇔ \(1⋮n^2+1\)
\(\Leftrightarrow n^2+1\inƯ\left(1\right)=\left\{1;-1\right\}\)
n
vậy khi n=1 phải không bạn