Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \({Q_1} = 56;{Q_3} = 84\)
\({\Delta _Q} = {Q_3} - {Q_1} = 84 - 56 = 28\)
\({Q_1} - 1,5{\Delta _Q} = 56 - 1,5.28 = 14\)
\({Q_3} + 1,5.{\Delta _Q} = 84 - 1,5.28 = 126\)
Ta thấy 10 < 14 nên 10 là giá trị bất thường

Sắp xếp lại mẫu số liệu:
20 120 20 120 21 315 23 405 37 546
Số trung bình:
\(\dfrac{{20120.2 + 21315 + 23405 + 37546}}{5}\)\( = 24501,2\)
Trung vị: 21 315
Mốt: 20 120
Nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình thì số trung bình giảm, trung vị giảm và Mốt thì vẫn giữ nguyên.
Cụ thể: số trung bình là 21 240; trung vị là 20 717,5 và Mốt vẫn là 20 120

Đáp án C
Dãy số liệu trên gồm 11 số. Do đó, số trung vị là: Me = x6 = 6,5

a) Sắp xếp theo thứ tự không giảm:
0 0 0 0 0 0 0 4 6 10
Số trung bình: \(\overline X = \dfrac{{0.7 + 4 + 6 + 10}}{{10}} = 2\)
Trung vị: \({Q_2} = 0\)
+ Mốt: 0
Tứ phân vị:
+ Nửa bên trái của \({Q_2}\):
0 0 0 0 0
=>\({Q_1} = 0\)
+ Nửa bên phải của \({Q_2}\):
0 0 4 6 10
=>\({Q_3} = 4\)
b) Tứ phân vị thứ nhất và trung vị trùng nhau vì mật độ của mẫu số liệu tập trung hết ở nửa trái của trung vị, mẫu số liệu bên trái có số liệu bằng 0 hết.

Chọn A.
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Số khách | 430 | 550 | 430 | 520 | 550 | 515 | 550 | 110 | 520 | 430 | 550 | 880 | Cộng: 6035 |
Đơn vị điều tra: Số khách đến tham quan một điểm du lịch trong 12 tháng
Kích thước mẫu của số liệu: 6035

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
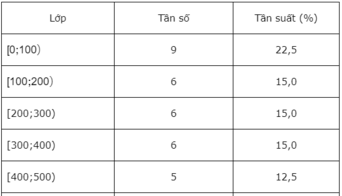
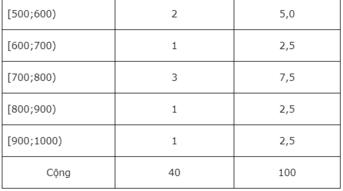
a) a) Nhìn vào bảng ta thấy lớp L 1 có tần số cao nhất. Đáp án là A.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
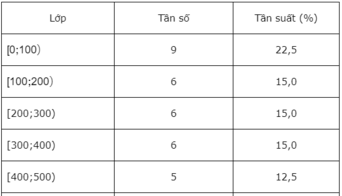
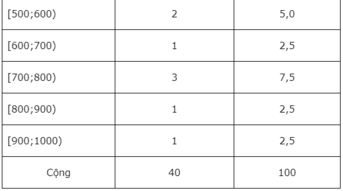
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.

a) Số trung bình \(\overline{x}=6,6\) triệu đồng. Số trung vị \(M_e=6\) triệu đồng. Mốt \(M_0=6\) triệu đồng
b) Trong các số liệu thống kê đã cho có sự chênh lệch nhau quá lớn, nên ta không chọn số trung bình cộng mà chọn số trung vị \(M_e=6\) triệu đồng, làm đại diện cho mức thu nhập trong năm 2000 của mỗi gia đình trong 31 gia đình được khảo sát.





Sắp xếp theo thứ tự không giảm.:
3,2 3,6 4,4 4,5 5,0 5,4 6,0 6,7 7,0 7,2 7,7 7,8 8,4 8,6 8,7
Vì n=15 nên \({Q_2} = 6,7\)
\({Q_1} = 4,5;{Q_3} = 7,8\)
\({\Delta _Q} = {Q_3} - {Q_1} = 7,8 - 4,5 = 3,3\)
\({Q_3} + 1,5.{\Delta _Q} = 12,75\)
\({Q_1} - 1,5{\Delta _Q} = - 0,45\)
Ta thấy không có giá trị nào dưới -0,45 và trên 12,75 nên không có giá trị bất thường.