Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có bảng
t (giờ) | 1 | 2 | 3 | 4 |
S (km) | 60 | 120 | 180 | 240 |
b) Với mỗi giá trị t, ta xác định được một giá trị tương ứng của S

Ta có các biểu thức:
\(s=vt;v=\dfrac{s}{t};t=\dfrac{s}{v}\)
Tất cả đều là đơn thức không phải đa thức
`S = v.t; v = S/t; t = S/v`.
Không phải là đa thức.

- Công thức tính thời gian di chuyển là: \(t = \frac{{150}}{v}\)
- Thời gian di chuyển t là một hàm số của vận tốc v
- Có v = 60 (km/h) => t = 2,5 (giờ)

Gọi độ dài quãng đường AB là x
Thời gian đi là x/35(h)
Thời gian về là x/40(h)
Theo đề ta có: \(\dfrac{x}{35}+\dfrac{x}{40}+\dfrac{1}{3}=8+\dfrac{1}{6}\)
\(\Leftrightarrow x\left(\dfrac{1}{35}+\dfrac{1}{40}\right)=8-\dfrac{1}{6}=\dfrac{47}{6}\)
hay x=1316/9

a) Quãng được vật đi được với vận tốc 3 \(km/h\)trong khoảng thời gian \(t\) (giờ) là:
\(s = v.t = 3.t\).
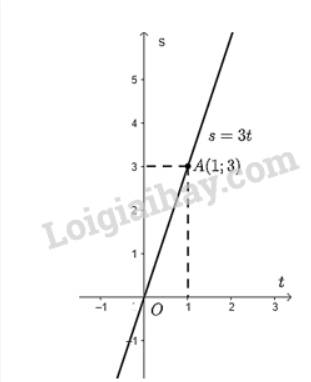
b) Vẽ đồ thị hàm số \(s = 3.t\)
Cho \(t = 1 \Rightarrow s = 3.1 = 3\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(M\left( {1;3} \right)\).
Đồ thị hàm số \(s = 3.t\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

\(v = 10 \Rightarrow t\left( {10} \right) = \dfrac{{20}}{{10}} = 2\);
\(v = 20 \Rightarrow t\left( {20} \right) = \dfrac{{20}}{{20}} = 1\);
\(v = 40 \Rightarrow t\left( {40} \right) = \dfrac{{20}}{{40}} = 0,5\);
\(v = 80 \Rightarrow t\left( {80} \right) = \dfrac{{20}}{{80}} = 0,25\).
Ta lập được bảng sau:
\(v\)
10
20
40
80
t
2
1
0,5
0,25