Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC có AB = AC = 13 cm nên tam giác ABC cân tại A
Suy ra: đường trung tuyến AM cũng là đường cao.
Suy ra: AM ⊥ BC
Ta có: MB = MC = 1/2 BC = 1/2 .10 = 5 (cm)
Trong tam giác vuông AMB có ∠(AMB) = 90o
Áp dụng định lý Pitago ta có:
AB2 = AM2 + MB2
Suy ra: AM2 = AB2 - MB2
= 132 - 52 = 169 - 25 = 144
Vậy AM = 12(cm)

Chú ý AM là đường cao, từ đó dùng Định lý Pytago tính được AM = 12 cm.

refer
a) Vì AH là đường trung tuyến của tam giác ABC cân tại A:
nên HB=HC
Xét tam giác AHB và tam giác AHC:
có:+AB=AC( tam giác ABC cân tại A)
+HB=HC(cmt)
+AH: cạnh chung
Vậy tam giác AHB=tam giác AHC(c.c.c)
b) Vì tam giác AHB=tam giác AHC(cmt)
nên: góc AHB=góc AHC=90 độ( 2 góc tương ứng )
c) HB=HC=BC2=102=5cmHB=HC=BC2=102=5cm
Áp dụng định lí Pytago vào tam giác ABH vuông tại H:
có: AB2=AH2+BI2AB2=AH2+BI2
hay:132=AH2+52132=AH2+52
⇒AH2=132−52⇒AH2=132−52
⇔AH=√132−52=12⇔AH=132−52=12
Vậy AH=12cm
a, Xét Δ AHB và Δ AHC, có :
AH là cạnh chung
AB = AC (Δ ABC cân tại A)
HB = HC (AH là đường trung tuyến của BC)
=> Δ AHB = Δ AHC (c.c.c)
b, Xét Δ ABC cân tại A, có :
AH là đường trung tuyến
=> AH là đường cao
=> \(\widehat{AHC}=\widehat{AHB}=90^o\)
c, đề kì dzậy

a: XétΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: M là trung điểm của BC nên MB=MC=8cm
=>AM=6cm
a, Xét Δ ABM và Δ ACM, có :
AB = AC (gt)
AM là cạnh chung
MB = MC (M là trung điểm BC)
=> Δ ABM = Δ ACM (c.c.c)
b, Ta có : AB = AC (gt)
=> Δ ABC cân tại A
Ta có :
Δ ABC cân tại A
Mà AM là trung tuyến
=> AM là đường cao
=> AM ⊥ BC
c, Ta có :
M là trung điểm
=> BC = 2MB
=> 16 = 2MB
=> MB = 8 (cm)
Xét Δ AMB vuông tại M, có :
\(AB^2=AM^2+MB^2\)
=> \(10^2=AM^2+8^2\)
=> \(36=AM^2\)
=> AM = 6 (cm)

Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: BM=CM=3cm
=>AM=4cm
c: Xét ΔHBC có
HM vừa là đường cao, vừa là trung tuyến
=>ΔHBC cân tại H

Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 5cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 132 - 52 = 144 ⇒ AM = 12cm. Chọn A
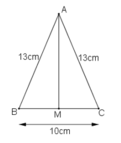

M 13CM 13cm 10cm A B C
Tam giác ABC có AC=AB=13cm nên tam giác ABC cân tại A
=>đường trung tuyến của AM cũng là đường cao
=>AM \(\perp BC\)
Ta có MB=MC=1/2BC=1/2.10=5(cm)
Trong tam giác vuông AMB có góc vuông AMB=\(90^0\)
Áp dụng định lý Pitago ta có:
\(AB^2=AM^2+MB^2\)
=>\(AM^2=ÂB^2-MB^2\)
=\(13^2-5^2=169-25=144\)
Vậy AM=12 (cm)