Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/5=b/6
=>a/20=b/24
b/8=c/9
=>b/24=c/27
c/3=d/2
=>c/27=d/18
=>a/20=b/24=c/27=d/18
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{20}=\dfrac{b}{24}=\dfrac{c}{27}=\dfrac{d}{18}=\dfrac{c-d}{27-18}=\dfrac{54}{9}=6\)
Do đó: a=120; b=144; c=162; d=108
\(A=a+2b+3c+4d=120+288+486+432=1326\)

Ta có:
\(\frac{2a}{3}=\frac{3b}{4}\Rightarrow\frac{2a}{3}:6=\frac{3b}{4}:6\)
\(\Rightarrow\frac{a}{9}=\frac{b}{8}\Rightarrow\frac{a}{27}=\frac{b}{24}\) ( 1 )
\(\frac{1}{4}\left(2b\right)=\frac{1}{5}\left(-3c\right)\Rightarrow\frac{b}{2}=\frac{-3c}{5}\Rightarrow\frac{b}{2}:3=-\frac{3c}{5}:3\)
\(\Rightarrow\frac{b}{6}=\frac{c}{-5}\Rightarrow\frac{b}{24}=\frac{c}{-20}\) (2 )
Từ (1) và ( 2) có:
\(\frac{a}{27}=\frac{b}{24}=\frac{c}{-20}\)
\(\Rightarrow\frac{a}{27}=\frac{2b}{48}=\frac{3c}{-60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{27}=\frac{2b}{48}=\frac{3c}{-60}=\frac{a-2b+3c}{27-48+\left(-60\right)}=\frac{1}{-81}\)
\(\Rightarrow\frac{a}{27}=\frac{b}{24}=\frac{c}{-20}=-\frac{1}{81}\)
\(\Rightarrow a-b-c=-\frac{1}{81}\left[27-24-\left(-20\right)\right]=-\frac{1}{81}.23=-\frac{23}{81}\)

a, Với x = 1 thì y = -3 . 1 = -3
Ta được A\((1;-3)\in\)đồ thị hàm số y = -3x
Đường thẳng OA là đồ thị hàm số y = -3x
y x 3 2 1 O 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -3 A y=-3x
b, Thay \(A(3;9)\)vào đồ thị hàm số y = -3x ta có :
y = -3 . 3 = -9 \(\ne\)9 Đẳng thức sai
Vậy điểm A ko thuộc đồ thị hàm số y = -3x
c, Thay tung độ bằng 4 ta có : \(4=-3\cdot x\)=> \(x=-\frac{4}{3}\)
Do đó ta tìm được hoành độ là -4/3 , tung độ là 4
Vậy tọa độ của điểm B là \(\left[-\frac{4}{3};4\right]\)
Bạn tìm tọa độ điểm B nhé
3.Ta có : y tỉ lệ nghịch với x theo hệ số tỉ lệ là 2 nên \(y=\frac{2}{x}\)
z tỉ lệ nghịch với y theo hệ số tỉ lệ là 3 nên \(z=\frac{3}{y}\)
Do đó \(\frac{2}{x}\cdot z=y\cdot\frac{2}{y}\Rightarrow x=\frac{2}{3}\cdot z\)
Vậy x tỉ lệ thuận với z theo hệ số tỉ lệ là \(\frac{2}{3}\)

a) Theo đề bài ta có: x+y+z=456; \(\frac{x}{3}=\frac{y}{5};\frac{y}{4}=\frac{z}{5}\)
Từ \(\begin{cases}\frac{x}{3}=\frac{y}{5}\\\frac{y}{4}=\frac{z}{5}\end{cases}\)=>\(\begin{cases}\frac{x}{12}=\frac{y}{20}\\\frac{y}{20}=\frac{z}{25}\end{cases}\)=>\(\frac{x}{12}=\frac{y}{20}=\frac{z}{25}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{12}=\frac{y}{20}=\frac{z}{25}=\frac{x+y+z}{12+20+25}=\frac{456}{57}=8\)
\(\Rightarrow\begin{cases}x=8.12=96\\y=8.20=160\\z=8.25=200\end{cases}\)
Vậy ...............................
b)Theo đề bài ta có: a+b+c+d=210; \(\frac{a}{2}=\frac{b}{3};\frac{b}{4}=\frac{c}{5};\frac{c}{6}=\frac{d}{7}\)
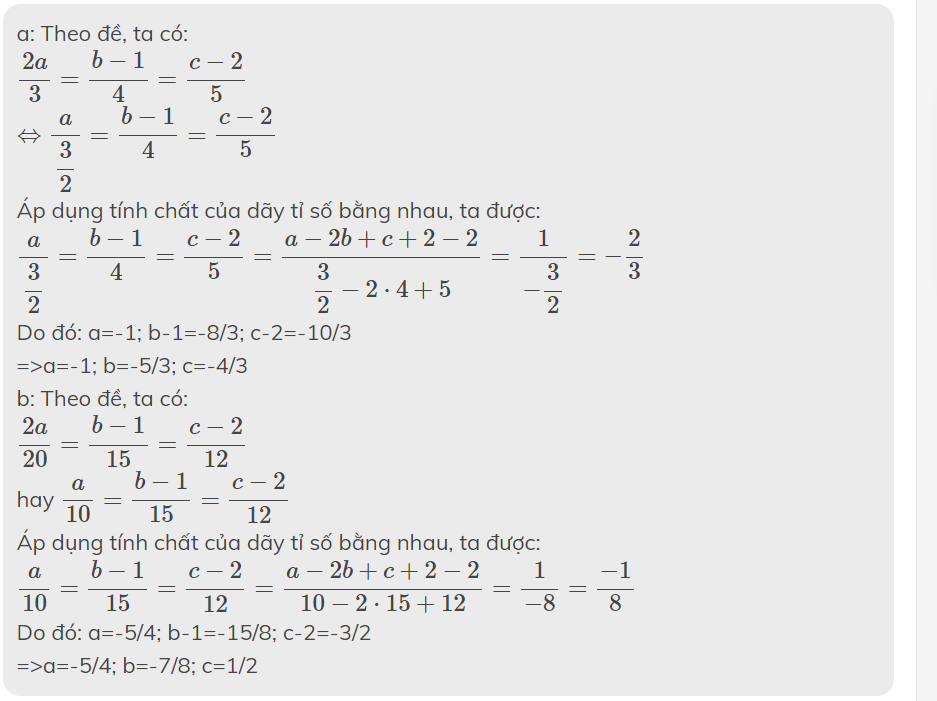
Ta có :
\(\frac{a}{b}=\frac{5}{6}\Rightarrow\frac{a}{b}=\frac{20}{24}\Rightarrow\frac{a}{20}=\frac{b}{24}\)\(\left(1\right)\)
\(\frac{b}{c}=\frac{8}{9}\Rightarrow\frac{b}{c}=\frac{24}{27}\Rightarrow\frac{b}{24}=\frac{c}{27}\)\(\left(2\right)\)
\(\frac{c}{d}=\frac{3}{2}\Rightarrow\frac{c}{d}=\frac{27}{18}\Rightarrow\frac{c}{27}=\frac{d}{18}\)\(\left(3\right)\)
Từ ( 1 ) ; ( 2 ) ; ( 3 ) \(\Rightarrow\frac{a}{20}=\frac{b}{24}=\frac{c}{27}=\frac{d}{18}=\frac{d-c}{18-24}=\frac{54}{-6}=-9\)
\(\frac{a}{20}=-9\Rightarrow a=-9.20=-180\)
\(\frac{b}{24}=-9\Rightarrow b=-9.24=-216\)
\(\frac{c}{27}=-9\Rightarrow c=-9.27=-243\)
\(\frac{d}{18}=-9\Rightarrow d=-9.18=-162\)
\(\Rightarrow A=a+2b+3c+4d=-180+\left(-216\right).2+\left(-243\right).3+\left(-162\right).4\)
\(=-1989\)