Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

Đáp án D
+ Chuẩn hóa 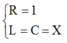
+ Hai giá trị của tần số góc cho cùng giá trị công suất
: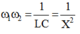
+ Tần số góc để điện hấp hiệu dụng ở hai đầu cuộn cảm đạt cực đại:

Ta có: 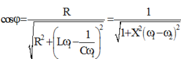
Mặc khác
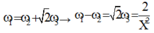
→ Thay vào biểu thức trên ta thu được
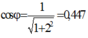

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

Chuẩn hóa R = 1 ⇒ L = C = X
Hai giá trị của tần số góc cho cùng giá trị công suất : ω 1 ω 2 = 1 L C = 1 X 2
Tần số góc để điện hấp hiệu dụng ở hai đầu cuộn cảm đạt cực đại: ω 3 2 = 1 L C − R 2 C 2 2 = 2 X 2
Ta có: cos φ = R R 2 + L ω 1 − 1 C ω 1 2 = 1 1 + X 2 ω 1 − ω 2 2
Mặc khác ω 1 = ω 2 + 2 ω 3 ⇒ ω 1 − ω 2 = 2 ω 3 = 2 X 2
Thay vào biểu thức trên ta thu được cos φ = 1 1 + 2 2 = 0 , 447
Đáp án B

Đáp án D
ω thay đổi, cosφ bằng nhau => ta có công thức ![]()
ω thay đổi, uL max ![]() Theo đề bài ta có
R
2
C
2
= LC nên suy ra
Theo đề bài ta có
R
2
C
2
= LC nên suy ra ![]()
Từ đó, kết hợp với đề bài ta có hệ 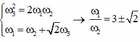
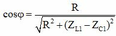
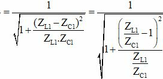
Lại có 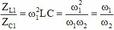 . Thay cả 2 trường hợp vào cosφ, ta đều tìm được
. Thay cả 2 trường hợp vào cosφ, ta đều tìm được
![]() .
.

Đáp án A
Phương pháp: Sử dụng các biến đổi toán học và bài toán f biến thiên
Cách giải: Ta có
![]()
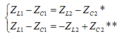
Xét **
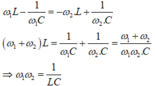
Tính toán tương tự ta loại * Khi thay đổi đến tần số f3 thì UL cực đại, khi đó
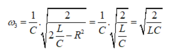
⇒ ω 1 . ω 2 = ω 2 3 2
Mà đề bài cho ta biết
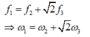
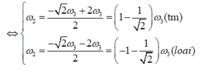
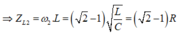
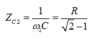
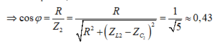

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
u u i i 120° 120°
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)
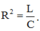
Giải thích: Đáp án C
Theo đề bài: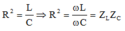
Chuẩn hóa: R=1 và đặt các thông số như sau:
Từ (1) và (2) ta có:
Giải hệ (3) + (4) + (5) ta được: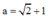
Thay a vào biểu thức cosφ