Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(-\frac{b}{2a}=-\frac{3}{2}\Leftrightarrow\frac{b}{2}=-\frac{3}{2}\Rightarrow b=-3\)
Phương trình (P): \(y=-x^2-3x+c\)
Thay tọa độ đỉnh \(x=-\frac{3}{2};y=\frac{1}{4}\) vào ta được:
\(\frac{1}{4}=-\frac{9}{4}+\frac{9}{2}+c\Rightarrow c=-2\)
\(\Rightarrow b+c=-5\)

Từ đề bài ta có:
\(\left\{{}\begin{matrix}-\frac{b}{2a}=\frac{1}{2}\\\frac{4ac-b^2}{4a}=\frac{3}{4}\\a+b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-b\\4ac-b^2=3a\\a+b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c=1\\a=1\\b=-1\end{matrix}\right.\)
Bạn tự vẽ đồ thị

1/ Đề đúng phải là \(3x^2+2y^2\) có giá trị nhỏ nhất nhé.
Áp dụng BĐT BCS , ta có
\(1=\left(\sqrt{2}.\sqrt{2}x+\sqrt{3}.\sqrt{3}y\right)^2\le\left[\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2\right]\left(2x^2+3y^2\right)\)
\(\Rightarrow2x^2+3y^2\ge\frac{1}{5}\). Dấu "=" xảy ra khi \(\begin{cases}\frac{\sqrt{2}x}{\sqrt{2}}=\frac{\sqrt{3}y}{\sqrt{3}}\\2x+3y=1\end{cases}\) \(\Leftrightarrow x=y=\frac{1}{5}\)
Vậy \(3x^2+2y^2\) có giá trị nhỏ nhất bằng 1/5 khi x = y = 1/5
2/ Áp dụng bđt AM-GM dạng mẫu số ta được
\(6=\frac{\left(\sqrt{2}\right)^2}{x}+\frac{\left(\sqrt{3}\right)^2}{y}\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{x+y}\)
\(\Rightarrow x+y\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{6}\)
Dấu "=" xảy ra khi \(\begin{cases}\frac{\sqrt{2}}{x}=\frac{\sqrt{3}}{y}\\\frac{2}{x}+\frac{3}{y}=6\end{cases}\) \(\Rightarrow\begin{cases}x=\frac{2+\sqrt{6}}{6}\\y=\frac{3+\sqrt{6}}{6}\end{cases}\)
Vậy ......................................

mình nghĩ pt (P) : y = ax^2 - bx + c chứ ?
a, (P) đi qua điểm A(0;-1) <=> \(c=-1\)
(P) đi qua điểm B(1;-1) <=> \(a-b+c=-1\)(1)
(P) đi qua điểm C(-1;1) <=> \(a+b+c=1\)(2)
Thay c = -1 vào (1) ; (2) ta được : \(a-b=0;a+b=2\Rightarrow a=1;b=1\)
Vậy pt Parabol có dạng \(x^2-x-1=y\)
Bài 1b
(P) đi qua điểm A(8;0) <=> \(64a-8b+c=0\)
(P) có đỉnh I(6;12) \(\Rightarrow\hept{\begin{cases}-\frac{b}{2a}=6\\36a-6b+c=-12\end{cases}}\Rightarrow a=3;b=-36;c=96\)
Vậy pt Parabol có dạng : \(9x^2+36x+96=y\)
tương tự nhé

Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}a\cdot0+b\cdot0+c=1\\-\dfrac{b}{2a}=\dfrac{1}{2}\\-\dfrac{b^2-4ac}{4a}=\dfrac{3}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=1\\b=-2a\\-b^2-4a=3a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=1\\b=-2a\\-4a^2-4a-3a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=1\\a=-\dfrac{7}{4}\\b=\dfrac{7}{2}\end{matrix}\right.\)
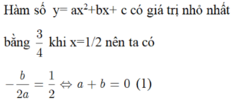
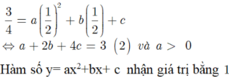
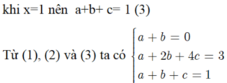
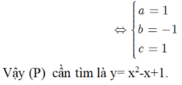
Đáp án D