Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(i_1=3,5/7=0,5mm\)
\(i_2=7,2/8=0,9mm\)
Vân sáng: \(i=\dfrac{\lambda D}{a}\)
Suy ra: \(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}\Rightarrow \lambda_2=\lambda_1.\dfrac{i_2}{i_1}=420.\dfrac{0,9}{0,5}=756nm\)

o 1,2 1,2,3 x T
Khoảng cách giữa 2 vân gần nhất có màu giống vân trung tâm là \(x_{\equiv}\)
\(\Rightarrow x_{\equiv}=k_1i_1=k_2i_2=k_3i_3\)\(\Rightarrow k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)(1)
Ta có: \(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{5}{4}\)
Vì trong khoảng giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm chỉ có một vị trí trùng nhau của các vân sáng ứng với hai bức xạ λ1, λ2 nên: \(\begin{cases}k_1=5.2=10\\k_2=4.2=8\end{cases}\)
Thay vào (1) ta có: \(10\lambda_1=8\lambda_2=k_3\lambda_3\)
λ3 có màu đỏ nên λ1 > λ2
\(\Rightarrow k_3<8\)
\(\Rightarrow k_3=7;5;3\)
+ \(k_3=7\Rightarrow\lambda_3=\frac{8}{7}\lambda_2=\frac{8}{7}.0,5=0,57\)
+ \(k_3=5\Rightarrow\lambda_3=\frac{8}{5}\lambda_2=\frac{8}{5}.0,5=0,8\)loại, vì ngoài bức xạ màu đỏ.
Vậy \(\lambda_3=0,57\mu m\), không có đáp án nào thỏa mãn :))
Ý này của bạn bị nhầm λ3 có màu đỏ nên λ1 > λ2
Sửa lại là: Vì \(\lambda_3\) có màu đỏ nên \(\lambda_3>\lambda_2\)

Khoảng cách giữa 2 vân sáng gần nhau nhất cùng màu với vân trung tâm: \(x_T=k_1i_1=k_2i_2\)(1)
\(\Rightarrow k_1\lambda_1=k_2\lambda_2\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,6}{0,48}=\frac{5}{4}\)
\(\Rightarrow\begin{cases}k_1=5\\k_2=4\end{cases}\)
Thay vào (1) \(x_T=5i_1=4i_2\)
Như vậy tại vị trí 2 vân trùng nhau kể từ vân trung tâm có vân bậc 5 của \(\lambda_1\) và bậc 4 của \(\lambda_2\)
Do đó, giữa 2 vân sáng cùng màu vân trung tâm có: 4 vân sáng λ1 và 3 vân sáng λ2.
Đáp án A.

Đổi đơn vị: \(\lambda_1=450n m= 0,45 \mu m.\)
\(\lambda_1=600n m= 0,6 \mu m.\)
Hai vân sáng trùng nhau khi \(k_1i_1=k_2i_2 \)
<=> \(\frac{k_1}{k_2}= \frac{i_1}{i_2}=>\frac{k_1}{k_2}= \frac{\lambda_1}{\lambda_2} =\frac{3}{4}\ \ (*)\)
Xét trong đoạn MN nên \(5,5 mm \leq x_s \leq 22mm. \)
<=> \(5,5 mm \leq k_1\frac{\lambda_1 D}{a} \leq 22mm. \)
<=> \(\frac{5,5.a}{\lambda_1 D} \leq k_1\leq \frac{22.a}{\lambda_1 D}\)
Giữ nguyên đơn vị của a = 0,5 mm; D = 2m; \(\lambda_1=0,45 \mu m.\)
<=> \(3,055 \leq k_1 \leq 12,22\)
Kết hợp với (*) ta có \(k_1\) chỉ có thể nhận giá trị : 3x2= 6; 3x3 = 9; 3x4 =12.
Như vậy có 3 vị trí trùng nhau của hai bức xạ trong đoạn MN.

\(i_1 = \frac{\lambda_1D_1}{a}\)
\(i_2 = \frac{\lambda_2D_2}{a}\)
=> \(\frac{i_1}{i_2} = \frac{\lambda_1D_1}{\lambda_2D_2} \)
=> \(\frac{\lambda_1}{\lambda_2} = \frac{i_1D_2}{i_2D_1} = \frac{1.2}{3.1}= \frac{2}{3}\) (do \(i_2 = 3i_1; D_2 = 2D_1\))
=> \(\lambda_2 = \frac{3\lambda_1}{2} = \frac{3.0,4}{2} = 0,6 \mu m.\)
Chọn đáp án.A

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.

\(x_s= k\frac{\lambda D}{a}.\)
\(d_2-d_1 = \frac{x_sa}{D}= k\lambda\)
=>\(k= \frac{d_2-d_1}{\lambda}=\frac{1,5.10^{-6}}{\lambda}.(1)\)
Thay các giá trị của bước sóng \(\lambda\)1, \(\lambda\)2,\(\lambda\)3 vào biểu thức (1) làm sao mà ra số nguyên thì đó chính là vân sáng của bước sóng đó.

Điều kiện vân trùng: \(k_1.\lambda_1=k_2.\lambda_2\)
\(\Rightarrow \lambda_2=\dfrac{k_1\lambda_1}{k_2}\)
Mặt khác \(k_1-1+k_2-1=9 ==> k_1+k_2=11 ==> k_1=11-k_2
\)
Ta có: \(0,38 \le \lambda_2 \le 0,76\)
==> \(0,38 \le \frac{11.\lambda_1}{k_2} - \lambda_1 \le 0,76\)
==> \(0,38 \le \frac{4,851}{k_2}-0,4410 \le 0,76\)
==> \(k_2<5,9 ; k_2>4,03 ==> k=5 ==> \lambda_2=6.\lambda_1/5=5292A^o\)

Đáp án D
Phương pháp: Coi sự giao thoa trùng vân giống như giao thoa ánh sáng đơn sắc, ta đi tìm khoảng vân trùng nhau.
Cách giải:
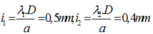
Vị trí vân sáng và vân tối thỏa mãn điều kiện :
![]()
Vì vân sáng trùng với vị trí vân tối nên ta có:
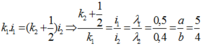
Coi đây là hiện tượng giao thoa với khoảng vân trùng nhau là:
![]()
Số vân trùng nhau trong khoảng MN thỏa mãn điều kiện :
![]()
![]()
![]()
Vậy có 15 giá trị k thỏa mãn
+ Khi vân sang của bức xạ λ 1 trùng với vân tối của bức xạ λ 2
k 1 k 2 + 0 , 5 = λ 2 λ 1 = 2 2 , 5 = 6 7 , 5 = ...
i 2 = λ 2 D a = 0 , 75 m m
+ Trên đoạn MN có 4 vị trí vân sáng của bức xạ λ 1 trùng với vân tối của bức xạ λ 2