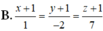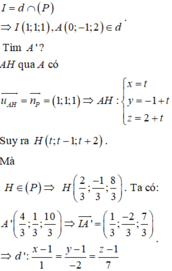Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi \(\overrightarrow{u}\left(1;-2;-1\right)\) là vectơ chỉ phương của d, giả sử \(\overrightarrow{v}\left(a;b;c\right)\) là 

14.
Mặt phẳng (P) nhận \(\overrightarrow{n}=\left(2;1;-2\right)\) là 1 vtpt
Đường thẳng d nhận \(\overrightarrow{u}=\left(1;-2;3\right)\) là 1 vtcp
Điểm \(M\left(2;0;-3\right)\) thuộc d nên cũng thuộc (Q)
(Q) vuông góc (P) và chứa d nên nhận \(\left[\overrightarrow{n};\overrightarrow{u}\right]=\left(1;8;5\right)\) là 1 vtpt
Phương trình (Q):
\(1\left(x-2\right)+8y+5\left(z+3\right)=0\)
\(\Leftrightarrow x+8y+5z+13=0\)
15.
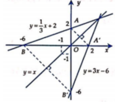
Phương trình hoành độ giao điểm:
\(sinx=cosx\Rightarrow x=\frac{\pi}{4}\)
\(S=\int\limits^{\frac{\pi}{4}}_0\left(cosx-sinx\right)dx+\int\limits^{\pi}_{\frac{\pi}{4}}\left(sinx-cosx\right)dx=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}\)
10.
Coi lại đề nào bạn, pt hình phẳng (D) có vấn đề, nhìn chữ -dx+4 kia ko biết phải nghĩ sao
11.
Cũng ko dịch được đề này, đoán đại: cho \(F\left(x\right)=x^2\) là 1 nguyên hàm của \(f\left(x\right).e^{2x}\). Tìm nguyên hàm của \(f'\left(x\right).e^{2x}\)
\(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=e^{2x}f\left(x\right)-2\int f\left(x\right)e^{2x}dx=e^{2x}f\left(x\right)-2x^2+C\)
12.
Đúng là \(y=\left(e+1\right)x\) và \(y=1+e^x\) chứ bạn? Hai đồ thị này cắt nhau tại 2 điểm, nhưng ko thể tìm được tọa độ của điểm thứ 2 đâu
13.
Hình chiếu của A lên Ox có tọa độ \(\left(1;0;0\right)\)

\(d:\frac{x}{1}=\frac{y+1}{2}=\frac{z-1}{-2}\) có VTCP \(\overrightarrow{u}\left(1;2;-2\right)\)
Mặt phẳng \(\left(Oxz\right)\)có VTPT \(\overrightarrow{j}\left(0;1;0\right)\)
Mặt phẳng (P) chứa d và vuông góc với (Oxz) nên VTPT của (P) là:
\(\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{j}\right]=\left(2;0;1\right)\)
Mặt phẳng (P): điểm \(M\left(0;-1;1\right)\in d\subset\left(P\right)\), VTPT \(\overrightarrow{n}\left(2;0;1\right)\)
\(\Rightarrow\left(P\right):2x+z-1=0\)

Đường thẳng d đi qua A (1; 1; 9) và có vectơ chỉ phương \(\overrightarrow{a}\left(1;1;0\right)\). Gọi (Q) là mặt phẳng đi qua d và vuông góc với (P)


a) Xét mặt phẳng (P) đi qua d và (P) ⊥ (Oxy), khi đó ∆ = (P) ∩ (Oxy) chính là hình chiếu vuông góc của d lên mặt phẳng (Oxy).
Phương trình mặt phẳng (Oxy) có dạng: z = 0 ; vectơ (0 ; 0 ;1) là vectơ pháp tuyến của (Oxy), khi đó
và
( 1 ; 2 ; 3) là cặp vectơ chỉ phương của mặt phẳng (P).
= (2 ; -1 ; 0) là vectơ pháp tuyến của (P).
Phương trình mặt phẳng (P) có dạng:
2(x - 2) - (y + 3) +0.(z - 1) = 0
hay 2x - y - 7 = 0.
Đường thẳng hình chiếu ∆ thỏa mãn hệ:
Điểm M0( 4 ; 1 ; 0) ∈ ∆ ; vectơ chỉ phương của ∆ vuông góc với
và vuông góc với
, vậy có thể lấy
= (1 ; 2 ; 0).
Phương trình tham số của hình chiếu ∆ có dạng:
.
Chú ý :
Ta có thể giải bài toán này bằng cách sau:
Lấy hai điểm trên d và tìm hình chiếu vuông góc của nó trên mặt phẳng (Oxy). Đường thẳng đi qua hai điểm đó chính là hình chiếu cần tìm.
Chẳng hạn lấy M1( 2 ; 3 ; -1) ∈ d và M2( 0 ; -7 ; -5) ∈ d, hình chiếu vuông góc của
M1 trên (Oxy) là N1 (2 ; -3 ; 0), hình chiếu vuông góc của M2 trên (Oxy) là N2(0 ; -7 ; 0).
Đườn thẳng ∆ qua N1, N2 chính là hình chiếu vuông góc của d lên (Oxy).
Ta có : (-2 ; -4 ; 0) //
(1 ; 2 ; 0).
Phương trình tham số của ∆ có dạng:
.
b) Tương tự phần a), mặt phẳng (Oxy) có phương trình x = 0.
lấy M1( 2 ; 3 ; -1) ∈ d và M2( 0 ; -7 ; -5) ∈ d, hình chiếu vuông góc của
M1 trên (Oxy) là M'1 (0 ; -3 ; 1), hình chiếu vuông góc của M2 trên (Oyz) là chính nó.
Đườn thẳng ∆ qua M'1, M2 chính là hình chiếu vuông góc của d lên (Oyz).
Ta có: (0 ; -4 ; -6) //
(0 ; 2 ; 3).
Phương trình M'1M2 có dạng:
.