

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án B
Vì ![]() mà
mà ![]()
Vì M là hình chiếu vuông góc của I trên ∆ ![]()
Khi đó 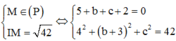
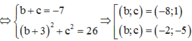
Vậy M(5; - 2; - 5) hoặc M(5; - 8;1) → bc=10

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

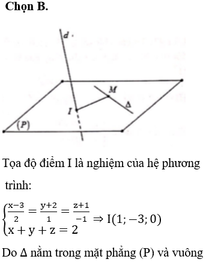
Ta có phương trình tham số của d là:
d : x - 3 2 = y + 2 1 = z + 1 - 1
Suy ra tọa độ điểm M là nghiệm của phương trình:
3 + 2t - 2 + t - 1 - t + 2 = 0 nên t = -1 nên M ( 1;-2;0 )
Lại có VTPT của (P) là n P → 1 ; 1 ; 1 , VTCP của d là u d → 2 ; 1 ; - 1
Vì ∆ nằm trong (P) và vuông góc với d nên VTCP u ∆ → = u d → ; n p → = 2 ; 3 ; - 1
Gọi N ( x;y;z ) là hình chiếu vuông góc của M trên ∆ , khi đó M N → x - 1 ; y + 3 ; z
Ta có M N → vuông góc với u ∆ → nên ta có hệ phương trình: 2x - 3y + z - 11 = 0
Lại có N ∈ P và MN = 42 ta có hệ:
x + y + z = 2 2 x - 3 y + z - 11 = 0 x - 1 2 + y - 3 2 + z 2 = 42
Giải hệ ta tìm được hai nghiệm ( x;y;z ) là ( 5;-2;-5 ) và ( -3;-4;5 )
- Nếu N ( 5;-2;-5 ) ta có phương trình
∆ : x - 5 2 = y + 2 - 3 = z + 5 1
- Nếu N ( -3;-4;5 ) ta có phương trình
∆ = x + 3 2 = y + 4 - 3 = z - 5 1
Đáp án D

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra