Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu điểm M thuộc đường thẳng ax + by = c thì tọa độ (xo; yo) của điểm M là một nghiệm của phương trình ax + by = c.

bài làm
a, gọi H là tiếp điểm của tiếp tuyến MN
theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
nên ta có: MN=HM=HN=\(\dfrac{1}{2}\)(AOH =HON)=90 độ
vậy góc MON=90 đọ và là tâm giác vuông tại O đường cao OH
b,theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông: OI^2=MI.INOH2=MH.HNAM.BN=MI.NI=OI^
Vì vậy AM.BN=MI.NI=OI^2=R^2AM.BN=MH.NH=
\(OH^2\)=\(R^2\)

Câu 2:
a: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nen DM=DB và OD là phân giác của góc MOB(2)
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ
b: DM=DB
OB=OM
DO đó:OD là đường trung trực của MB
=>OD vuông góc với MB(3)
c: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM vuông góc với MB(4)
Từ (3) và (4) suy ra AM//OD

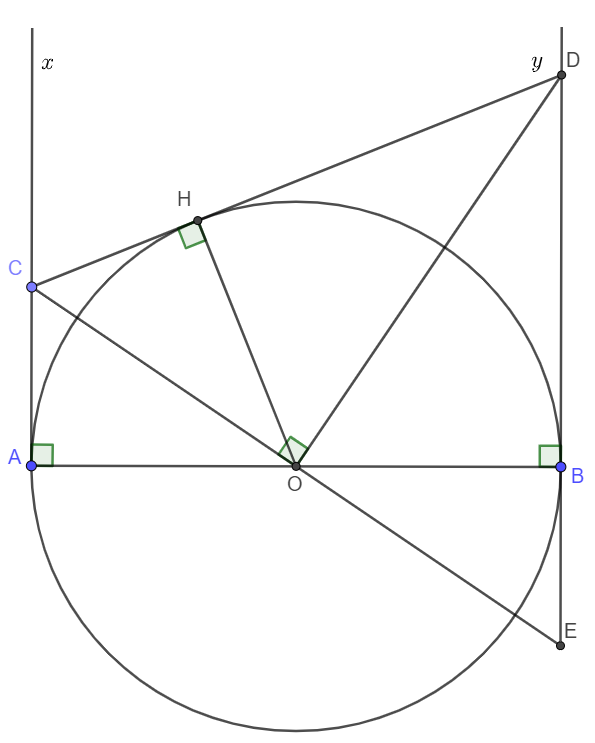
Vẽ OH\perp CD\left(H\in CD\right)OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OEΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH\perp DC,OB\perp DE\Rightarrow OH=OB.OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH\perp CD,OH=OB=rOH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).
Vẽ OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có ΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).



Nếu điểm M thuộc đường thẳng ax + by = c thì tọa độ ( x 0 ; y 0 ) của điểm M là một nghiệm của phương trình ax + by = c.