Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Ta có y ' = - 3 x 2 + 3 m ; y ' = 0 ⇔ [ x = m ⇒ y = 2 m m + 1 ⇒ B ( m ; 2 m m + 1 ) x = - m ⇒ y = - 2 m m + 1 ⇒ A ( - m ; - 2 m m + 1 )
Do ABOE là hình bình hành nên A B = E O ⇒ 2 m = 4 4 m m = 32 ⇒ m = 4 .

Đáp án A.
Phương trình hoành độ giao điểm của c m và d : x 3 - 3 x 2 + ( m + 1 ) x + 1 = x + 1
⇔ x 3 - 3 x 2 + m x = 0 ⇔ x = 0 x 2 - 3 x + m = 0 *
Để c m cắt d tại ba điểm phân biệt P ( 0 ; 1 ) , M , N thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0 ⇔ 0 2 - 3 . 0 + m ≢ 0 ∆ = ( - 3 ) 2 - 4 m > 0 ⇔ m ≢ 0 m < 9 4
Giả sử M ( x 1 ; x 1 + 1 ) vàvới N ( x 2 ; x 2 + 1 ) là nghiệm của phương trình (*).
Theo định lý Vi-ét ta có x 1 + x 2 = 3 x 1 x 2 = m
Để tam giác OMN vuông tại O thì O M → . O N → = 0 ⇔ x 1 x 2 + ( x 1 + 1 ) ( x 2 + 1 ) = 0
⇔ 2 x 1 x 2 + ( x 1 + x 2 ) + 1 = 0 ⇔ 2 m + 4 = 0 ⇔ m = - 2 (thỏa mãn)

Đáp án A
Xét phương trình hoành độ giao điểm:
x + 1 2 x + 1 = m x + m + 1 2 ⇔ 4 m x 2 + 4 m x + m − 1 = 0 1
Phương trình (1) có 2 nghiệm x A ; x B ⇔ Δ ' = 4 m 2 − 4 m m − 1 = 4 m > 0 ⇔ m > 0.
Khi đó giao điểm của 2 đồ thị là A x A ; m x A + m + 1 2 ; B x B ; m x B + m + 1 2
với x A + x B = − 1 ; x A . x B = m − 1 4 m
Ta có O A 2 + O B 2 = x A 2 + m x A + m + 1 2 2 + x B 2 + m x B + m + 1 2 2 = m 2 + 2 m + 1 2 m = 1 + 1 2 m + 1 m ≥ 1 + 1 2 .2 = 2
( vì m > 0 , theo Cauchy ta có m + 1 m ≥ 2 . Dấu bằng xảy ra khi m = 1



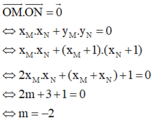
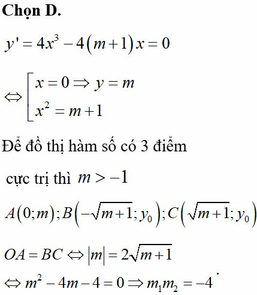

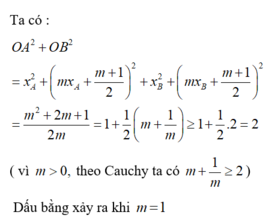
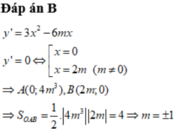
Đáp án B
Ta có: y ' = 4 x 3 - 4 m 2 x = 0 ⇔ [ x = 0 x = ± m . Hàm số có 3 cực trị khi m ≠ 0 . Khi đó A ( 0 ; 2 m ) ; B ( m ; 2 m - m 4 ) ; C - m ; 2 m - m 4 O,A,B,C là các đỉnh của một hình thoi suy ra O A = A B ⇔ m 2 + 2 m - m 4 2 = m 2 + m 8 ⇔ 4 m 2 - 4 m 5 = 0 ⇒ m = 1 .