Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow1}\frac{x^{2016}+x-2}{\sqrt{2018x+1}-\sqrt{x+2018}}=\lim\limits_{x\rightarrow1}\frac{2016x^{2015}+1}{\frac{1009}{\sqrt{2018x+1}}-\frac{1}{2\sqrt{x+2018}}}=\frac{2017}{\frac{1009}{\sqrt{2019}}-\frac{1}{2\sqrt{2019}}}=2\sqrt{2019}\)
Để hàm liên tục tại \(x=1\)
\(\Rightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow k=2\sqrt{2019}\)
2.
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax+b}{x^2-1}=\frac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}a+b+1=0\\\lim\limits_{x\rightarrow1}\frac{2x+a}{2x}=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=-1\\\frac{a+2}{2}=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\) \(\Rightarrow S=1\)
3.
\(\lim\limits_{x\rightarrow1}\frac{\sqrt{x^2+x+2}-2+2-\sqrt[3]{7x+1}}{\sqrt{2}\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\frac{\left(x-1\right)\left(x+2\right)}{\sqrt{x^2+x+2}+2}-\frac{7\left(x-1\right)}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}}{\sqrt{2}\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{1}{\sqrt{2}}\left(\frac{x+2}{\sqrt{x^2+x+2}+2}-\frac{7}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}\right)\)
\(=\frac{1}{\sqrt{2}}\left(\frac{3}{4}-\frac{7}{12}\right)=\frac{\sqrt{2}}{12}\)
\(\Rightarrow a+b+c=1+12+0=13\)

- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
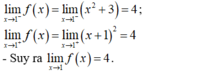
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
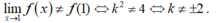
Chọn A

Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
![]()
suy ra ![]() .
.
Vậy để hàm số gián đoạn tại x = 1 khi ![]() ⇔ k2 ≠ 4 ⇔ k ≠ ±2.
⇔ k2 ≠ 4 ⇔ k ≠ ±2.


`f'(x) = x^2 - 4x+m`
`f'(x) >=0 <=>x^2-4x+m>=0`
`<=> \Delta' >=0`
`<=> 2^2-1.m>=0`
`<=> m<=4`
Vậy....
Chọn D.
Ta có:
Hàm số có giới hạn khi
⇔ a + 3 = 3a + 1 ⇔ a = 1.
Vậy a = 1 là giá trị cần tìm.