Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}
a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}

Ta có:
A = {15; 26}
B = {1; a; b}
M = {bút}
H = {sách; vở; bút}.
Bạn học lớp 6 à . Năm nay mình học lớp 7 nhưng vẫn nhớ bài Bài 4 trang 6 SGK Toán 6 tập 1 . Kb có gì khó hỏi mk nha


Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8

Bài 1 :
a) A=37.36+20.37+44.37
A=37.(36+20+44)
A=37.100
A=3700
Bài 6 :
\(A=2^0+2^1+2^2+2^3+...+2^{2010}\)
\(2A=2+2^2+2^3+2^4+...+2^{2011}\)
\(2A-A=\left(2+2^2+2^3+2^4+...+2^{2011}\right)-\left(2^0+2^1+2^2+2^3+...+2^{2010}\right)\)
\(A=\left(2+2^2+2^3+2^4+...+2^{2010}\right)+2^{2011}-2^0-\left(2+2^2+2^3+2^4+...+2^{2010}\right)\)
\(A=2^{2011}-1\)
\(\Rightarrow A+1=2^{2011}\)
Vậy A đã có dạng lũy thừa cơ số là 2


Gọi số học sinh khối 7 của trường đó là : b (học sinh)
Gọi số học sinh khối 8 của trường đó là : c (học sinh)
Gọi số học sinh khối 9 của trường đó là : d (học sinh)
Với điều kiện :a>0;b>0;c>;d>0 (*).
Theo đề bài, tổng số học sinh khối 6 và khối 7 chiếm \(\dfrac{25}{44}\) tổng số học sinh toàn trường,nên :
a+b= \(\dfrac{25}{44}\)\(\times\)1320=750 (1)
Số học sinh khối 8 chiếm 25% số học sinh toàn trường nên:
c=25% \(\times\)1320=330 (học sinh)
Số học sinh khối 8 là : d=1320 \(-\)(a+b)\(-\)c
= 1320 \(-\)750 \(-\)330 = 240 (học sinh)
Theo bài ra, tổng số học sinh khối 6 và khối 8 bằng 2 lần số học sinh khối 7 ,nên:
a+c=2b (2)
Từ (1)và (2) ,ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=750\\a+c=2b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-b\\750-b+330=2b\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=750-b\\1080-b=2b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-b\\-b-2b=-1080\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=750-b\\-3b=-1080\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-360=390\\b=360\end{matrix}\right.\)thỏa mản(*)
Vậy khối 6 có 390 (học sinh), khối 7có 360(học sinh), khối 8 có 330 (học sinh), khối 9 có 240 (học sinh).

Bài thi số 2 :
Câu 1 : Tập hợp các số có hai chữ số là bội của 32 là : { 32 ; 64 ; 96 }
Câu 2 :
Gọi tập hợp các số tự nhiên nhỏ hơn 120 chia hết cho 2 và 5 là : A
Thì ta được :
\(A=\left\{n\in N;0\le n< 120;n⋮10\right\}\)tập hợp A có 12 phần tử vì : ( 110 - 0 ) : 10 + 1 = 12
Câu 3 :
Gọi tập hợp đó là A thì ta được :
A = { 39 ; 52 ; 65 ; 78 ; 91 }
Tập hợp A có 5 phần tử
Câu 4 :
Tập hợp các số tự nhiên x sao cho \(6⋮\left(x-1\right)\) là : { 2 ; 3 ; 4 ; 7 }
Câu 5 :
Các số nguyên tố có dạng \(\overline{23a}\) : 233 ; 239
\(\Rightarrow\)Các hợp số có dạng \(\overline{23a}\) là : 230 ; 231 ; 232 ; 234 ; 235 ; 236 ; 237 ; 238
Vậy có 8 số
Câu 6 :
Các số nguyên tố có dạng \(\overline{13a}\) : 131 ; 137 ; 139
\(\Rightarrow\)Các hợp số có dạng \(\overline{13a}\) là : 130 ; 132 ; 133 ; 134 ; 135 ; 136 ; 138
Vậy có 7 số
Câu 7 :
Số p có một trong ba dạng : 3k, 3k + 1, 3k + 2 với \(k\in N^{\text{*}}\)Nếu p = 3k thì p = 3 (vì p là số nguyên tố), khi đó p + 2 = 5, p + 4 = 7 đều là các số nguyên tố.
Nếu p = 3k + 1 thì p + 2 = 3k + 3 chia hết cho 3 và lớn hơn 3 nên p + 2 là hợp số, trái với đề bài. Nếu p = 3k + 1 thì p + 4 = 3k + 6 chia hết cho 3 và lớn hơn 3 nên p + 4 là hợp số, trái với đề bài. Vậy p = 3 là giá trị duy nhất phải tìm.Câu 8 :
\(14⋮\left(2x+3\right)\)
\(\Rightarrow\)2x+3 là ước của 14
Ta có ước của 14 là 1,2,7,14
Vì x là số tự nhiên nên 2x+3\(\ge\)3
\(\Rightarrow\)Chọn 7 và 14
Với 2x+3=7 thì x=2
Với 2x+3=14 thì x=\(\dfrac{11}{2}\)(loại)
Vậy x=2
Câu 9 :
Số 1 và 2 cũng được
Số 2 và số 3 \(\Rightarrow\) Hiệu = 3 - 2 = 1
Số 2 và số 5 \(\Rightarrow\) Hiệu = 5 - 3 = 2
Số 2 và số 7 \(\Rightarrow\) Hiệu = 7 - 2 = 5
Số 2 và số 11 \(\Rightarrow\) Hiệu = 11 - 2 = 9
Vậy hiệu cũng là một số nguyên tố hoặc không
Câu 10 :
Tập hợp gồm tất cả các ước của 154 là: A = { 1 ; 2 ; 7 ; 11 ; 14 ; 22 ; 77 ; 154 }
Vì với một tập con B của A, mỗi phần tử của A có hai khả năng, thuộc B hoặc không thuộc B.
Do đó, với 8 phần tử sẽ có 28 tập hợp khác nhau.
Nên số tập hợp con của tập hợp A là 28 = 256 ( tập hợp con )
bài 2
19,36,54 nha
tại vì 9 x 2 =18 , 9 x 4 = 36 vậy 9 x 6 = 54
1) ko biết làm sorry nha
2) tập hợp A = { 10,20,30,....,110}vì số chia hết cho 2 và 5 là 0
3)tập hợp A = {39,52,65,78,91}
4)ko hiểu nha
5) ko hiểu
6) ko hiều
sorry nha mình biết làm mấy bài thôi nha like cho mình nha


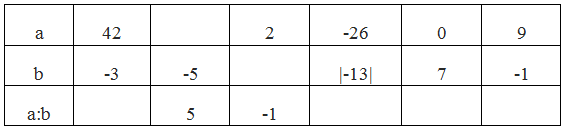
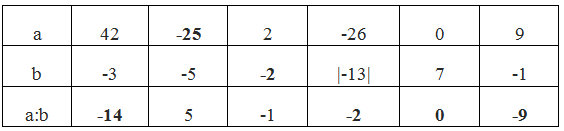
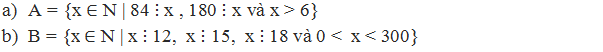
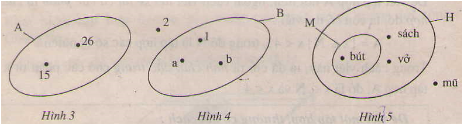

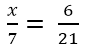
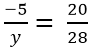

 giải hộ mk với
giải hộ mk với 



Tập hợp D = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 }
Điền kí hiệu thích hợp: 2 ∈ D; 10 ∉ D