Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (x, y > 0). Khi đó xy = 48. Theo bất đẳng thức Cô-si, ta có :
. Vậy chu vi hình chữ nhật nhỏ nhất bằng
(m) khi
(m), tức là khi hình chữ nhật là hình vuông.
Gọi hai cạnh hình chữ nhật: \(x,y\left(x,y>0\right)\).
Do diện tích hình chữ nhật: \(xy=48\Rightarrow y=\dfrac{48}{x}\).
Chu vi hình chữ nhật là: \(2\left(x+y\right)=2\left(x+\dfrac{48}{x}\right)=\dfrac{2\left(x^2+48\right)}{x}\).
Xét hàm số: \(y=\dfrac{2\left(x^2+48\right)}{x}\) với \(x\in\left(0;+\infty\right)\).
\(y'\left(x\right)=\dfrac{2\left(x^2-48\right)}{x^2}\)
\(y'\left(x\right)=0\)\(\Leftrightarrow x=4\sqrt{3}\).
Bảng biến thiên:
TenAnh1
TenAnh1
A = (-4.32, -5.92)
A = (-4.32, -5.92)
A = (-4.32, -5.92)
B = (11.04, -5.92)
B = (11.04, -5.92)
B = (11.04, -5.92)
C = (-4.38, -5.98)
C = (-4.38, -5.98)
C = (-4.38, -5.98)
D = (10.98, -5.98)
D = (10.98, -5.98)
D = (10.98, -5.98)
Từ bảng biến thiên ta ta thấy giá trị nhỏ nhất của \(y\left(x\right)=16\sqrt{3}\) với \(x_{GTNN}=4\sqrt{3}\).
Suy ra hình chữ nhật có chu vi nhỏ nhất khi \(x=y=4\sqrt{3}\).

Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).
⇒ độ dài cạnh còn lại : 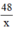 (m)
(m)
⇒ chu vi hình chữ nhật :
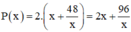
Xét hàm số 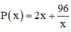 trên (0; +∞):
trên (0; +∞):
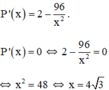
Bảng biến thiên trên (0; +∞):
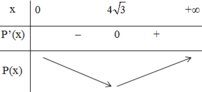
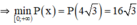
Vậy trong các hình chữ nhật có cùng diện tích 48m2 thì hình vuông cạnh 4√3 m có chu vi nhỏ nhất.

Chọn A.
Cách 1
Gọi cạnh của hình chữ nhật: a, b; 0 < a, b ≤ 48
Ta có, diện tích hình chữ nhật là 48 nên:
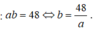
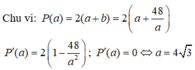
Bảng biến thiên:
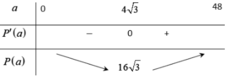
Cách 2
+) Áp dụng bất đẳng thức Côsi:
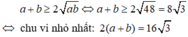
+) Hình chữ nhật có chu vi nhỏ nhất bằng 16 3 khi cạnh bằng 4 3

Phương pháp:
BĐT Cô si cho 2 số không âm a và b: ![]() dấu bằng xảy ra khi và chỉ khi a= b
dấu bằng xảy ra khi và chỉ khi a= b
Cách giải:
Giả sử hình chữ nhật có chiều dài, chiều rộng lần lượt là: ![]()
Theo đề bài ta có: ![]()
Diện tích của hình chữ nhật: 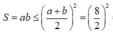
![]()
khi và chỉ khi a = b = 4
Chọn: C

Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:
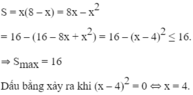
Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16 c m 2 .

Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:

Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16cm2.

Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 16). Khi đó x + y = 8. Theo bất đẳng thức Cô-si, ta có : 8 = x + y ≥ 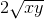 ⇔ xy ≤ 16.
⇔ xy ≤ 16.
xy =16 ⇔ x = y = 4. Vậy diện tích hình chữ nhật lớn nhất bằng 16 cm2 khi x = y = 4(cm), tức là khi hình chữ nhật là hình vuông.

Đáp án là C
Giả sử hình chữ nhật có chiều dài và chiều rộng lần lượt là a, b(0<a, b<150), đơn vị: m.
Từ giả thiết, ta có a+b=150
Diện tích hình chữ nhật là S=a.b
Cách 1:
Áp dụng bất đẳng thức Cô – si, ta có
a b ≤ a + b 2 ⇔ a b ≤ 75 ⇔ a b = 5625 ⇔ S = 5625
Dấu bằng xảy ra a = b a + b = 150 ⇔ a = 75 b = 75
Hay max S= 5625 m 2
Cách 2:
Ta có a+b=150 <=> b=150-a
Khi đó S=a.b=a(150-a)= - a 2 + 150 a
Xét hàm số f a = - a 2 + 150 a 0 < a < 150
f ' a = - 2 a + 150 , f ' a = 0 ⇔ a = 75
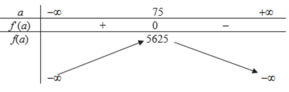
Vậy max S= 5625 m 2

Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:
Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16cm2.
Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).
⇒ độ dài cạnh còn lại :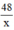 (m)
(m)
⇒ chu vi hình chữ nhật :
Xét hàm số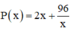 trên (0; +∞):
trên (0; +∞):
Bảng biến thiên trên (0; +∞):
Vậy trong các hình chữ nhật có cùng diện tích 48 m 2 thì hình vuông cạnh 4 3 m có chu vi nhỏ nhất.