Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (x, y > 0). Khi đó xy = 48. Theo bất đẳng thức Cô-si, ta có :
. Vậy chu vi hình chữ nhật nhỏ nhất bằng
(m) khi
(m), tức là khi hình chữ nhật là hình vuông.
Gọi hai cạnh hình chữ nhật: \(x,y\left(x,y>0\right)\).
Do diện tích hình chữ nhật: \(xy=48\Rightarrow y=\dfrac{48}{x}\).
Chu vi hình chữ nhật là: \(2\left(x+y\right)=2\left(x+\dfrac{48}{x}\right)=\dfrac{2\left(x^2+48\right)}{x}\).
Xét hàm số: \(y=\dfrac{2\left(x^2+48\right)}{x}\) với \(x\in\left(0;+\infty\right)\).
\(y'\left(x\right)=\dfrac{2\left(x^2-48\right)}{x^2}\)
\(y'\left(x\right)=0\)\(\Leftrightarrow x=4\sqrt{3}\).
Bảng biến thiên:
TenAnh1
TenAnh1
A = (-4.32, -5.92)
A = (-4.32, -5.92)
A = (-4.32, -5.92)
B = (11.04, -5.92)
B = (11.04, -5.92)
B = (11.04, -5.92)
C = (-4.38, -5.98)
C = (-4.38, -5.98)
C = (-4.38, -5.98)
D = (10.98, -5.98)
D = (10.98, -5.98)
D = (10.98, -5.98)
Từ bảng biến thiên ta ta thấy giá trị nhỏ nhất của \(y\left(x\right)=16\sqrt{3}\) với \(x_{GTNN}=4\sqrt{3}\).
Suy ra hình chữ nhật có chu vi nhỏ nhất khi \(x=y=4\sqrt{3}\).
Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).
⇒ độ dài cạnh còn lại :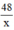 
(m)
⇒ chu vi hình chữ nhật :
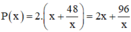
Xét hàm số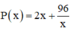 
trên (0; +∞):
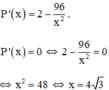
Bảng biến thiên trên (0; +∞):
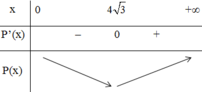
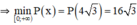
Vậy trong các hình chữ nhật có cùng diện tích 48 m 2 thì hình vuông cạnh 4 3 m có chu vi nhỏ nhất.
Chọn A.
Cách 1
Gọi cạnh của hình chữ nhật: a, b; 0 < a, b ≤ 48
Ta có, diện tích hình chữ nhật là 48 nên:
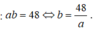
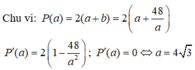
Bảng biến thiên:
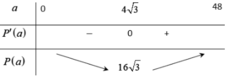
Cách 2
+) Áp dụng bất đẳng thức Côsi:
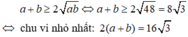
+) Hình chữ nhật có chu vi nhỏ nhất bằng 16 3 khi cạnh bằng 4 3
Phương pháp:
BĐT Cô si cho 2 số không âm a và b: 
dấu bằng xảy ra khi và chỉ khi a= b
Cách giải:
Giả sử hình chữ nhật có chiều dài, chiều rộng lần lượt là: 
Theo đề bài ta có: 
Diện tích của hình chữ nhật: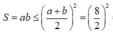 
khi và chỉ khi a = b = 4
Chọn: C
Chiều dài hình chữ nhật ban đầu là:
\(240\div16=15\left(m\right)\)
Nửa chu vi hình chữ nhật hay tổng chiều dài và chiều rộng là:
\(160\div2=80\left(m\right)\)
Chiều rộng hình chữ nhật ban đầu là:
\(80-15=65\left(m\right)\)
Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:
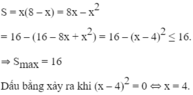
Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16 c m 2 .
Nửa chu vi hình chữ nhật là: 16 : 2 = 8cm.
Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)
⇒ độ dài cạnh còn lại là : 8 – x (cm)
⇒ Diện tích của hình chữ nhật là:
Vậy trong các hình chữ nhật có chu vi 16cm thì hình vuông cạnh bằng 4cm có diện tích lớn nhất bằng 16cm2.
Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 16). Khi đó x + y = 8. Theo bất đẳng thức Cô-si, ta có : 8 = x + y ≥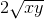 
⇔ xy ≤ 16.
xy =16 ⇔ x = y = 4. Vậy diện tích hình chữ nhật lớn nhất bằng 16 cm2 khi x = y = 4(cm), tức là khi hình chữ nhật là hình vuông.
Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).
⇒ độ dài cạnh còn lại :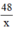
(m)
⇒ chu vi hình chữ nhật :
Xét hàm số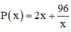
trên (0; +∞):
Bảng biến thiên trên (0; +∞):
Vậy trong các hình chữ nhật có cùng diện tích 48m2 thì hình vuông cạnh 4√3 m có chu vi nhỏ nhất.