Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Bước sóng: λ = v/f = 40/20 = 20(cm)
+ Vì hai nguồn ngược pha và điểm M thuộc cực đại nên: MA – MB = (k + 0,5)λ
+ Điểm M gần A nhất khi M thuộc đường cực đại gần A nhất.
+ Số cực đại trên AB:
- AB λ - 1 2 < k < AB λ - 1 2
=> - 8,5 < k < 7,5 => điểm M thuộc k = - 8
=> MA – MB = -15 => MB = MA + 15 (1)
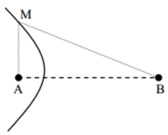
+ Trong tam giác vuông AMB ta có:
MB2 = MA2 + AB2 , từ (1) ta có (MA + 15)2 = MA2 + 162 => MA ≈ 1,033 cm .

Đáp án D
+ Bước sóng: ![]()
+ Vì hai nguồn ngược pha và điểm M thuộc cực đại nên: MA – MB = (k + 0,5)λ
+ Điểm M gần A nhất khi M thuộc đường cực đại gần A nhất.
+ Số cực đại trên AB: ![]()
=> - 8,5 < k < 7,5 => điểm M thuộc k = - 8
=> MA – MB = -15 => MB = MA + 15 (1)
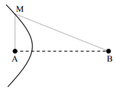
+ Trong tam giác vuông AMB ta có:
MB2 = MA2 + AB2,
từ (1) ta có (MA + 15)2 = MA2 + 162
=> MA ≈ 1,033 cm.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Số điểm cực đại trên đoạn AG là số giá trị k thỏa mãn \(-AG \leq (k+\frac{\triangle \phi}{2\pi})\lambda \leq AG \Rightarrow -\frac{AB}{4}.3=10.875cm \leq (k+0.5)\lambda \leq 10.875\\ \Rightarrow -5.94 \leq k \leq 4.94 \Rightarrow k = -5,-4,\ldots,0,1,\ldots,4\)
có 10 điểm dao động cực đại trên đoạn AG

Đáp án C
+ Điều kiện để có cực đại giao thoa với hai nguồn ngược pha
∆ d = d 2 - d 1 = ( k + 0 , 5 ) λ .
Với khoảng giá trị của ∆ d :
0 - 14 , 5 cm < ∆ d < 10 , 875 - 3 , 625 cm → - 7 , 75 ≤ k ≤ 3 , 125 .
→ Có 11 điểm dao động với biên độ cực đại.

Xem Hình II.5G.
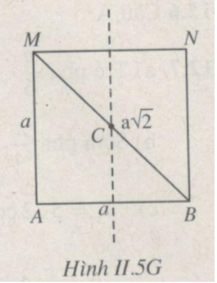
Trước hết ta tìm số vân cực đại trên toàn mặt thoáng. Đó cũng là số vân cực đại trên đoạn AB. Vì hai nguồn kết hợp dao động ngược pha nên ta có :
d 1 - d 2 = (k + 1/2) λ
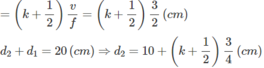
Vì 0 < d 2 < 20 (cm) ⇒ k = -13,..., -12, -1,0, 1.., 12
Bây giờ ta xét số vân cực đại trên đoạn BM.
-20 < d 2 - d 1 < 20( 2 - 1)(cm)
-20 < (k + 1/2).3/2 ≤ 2 - ( 2 - 1)
⇒ k = -13, -12 ...-1.0, 1,..., 5 ⇒ 19 điểm.

Chọn đáp án C
ta có lamda= 4cm. để MA min thì M phải thuộc cực tiểu xa đường trung trực nhất. xét -AB/4-1/2<= K <=
AB/4-1/2 => -4,75<= K <=3,75. => k= -4.
M thuộc cực tiểu nên MA-MB= (2k+1).lamda/2 <=>d1- căn( d1^2 + AB^2}= (2.-4 +1)2 <=>d1= 3,32

Chọn đáp án B
Đặt A B = l = 50 c m , bước sóng λ = v . T = 8 c m .
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
− l λ < k < l λ ⇒ − 6,25 < k < 6,25 ⇒ k = 0, ± 1,...., ± 6.
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒MA = MB + 48 (cm). MB⊥AB
⇒ M A 2 = A B 2 + M B 2 ⇔ ( M B + 48 ) 2 = A B 2 + M B 2 ⇔ M B 2 + 96 M B + 48 2 = 50 2 + M B 2 ⇔ M B = 50 2 − 48 2 96 = 2,04 c m

Đáp án D
+ Bước sóng: λ = v f = 40 20 = 2 c m
+ Vì hai nguồn ngược pha nên điều kiện cực đại cho M là: M A − M B = k + 0 , 5 λ = 2 k + 1
+ Vì M gần A nhất nên M phải thuộc cực đại ngoài cùng về phía A.
+ Số cực đại trên AB: − A B λ − 1 2 < k < A B λ − 1 2
⇒ − 8 , 5 < k < 8 , 5 ⇒ k = − 8
⇒ M A − M B = 2 − 8 + 1 = − 15 ⇒ M B = M A + 15 1
+ Vì Δ A M B vuông tại A nên: M A 2 + A B 2 = M B 2 2
+ Thay (1) vào (2) ta có: M A 2 + 16 2 = M A + 15 2 ⇒ M A = 1 , 03 c m