Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Tổng số trận đấu trong giải đấu là: ![]()
Sau mỗi trận hòa, tổng số điểm 2 đội nhận được là 1.2 =2.
Sau mỗi trận không hòa, tổng số điểm 2 đội nhận được là 3 + 0 = 3.
Tổng số điểm của tất cả các đội sau khi kết thúc giải đấu là:
65.2 + (182 – 65).3 = 481.

Đáp án A
Số vòng đấu là ![]() vòng đấu (gồm cả lượt đi và về)
vòng đấu (gồm cả lượt đi và về)
Mỗi vòng đấu có 7 trận đấu
Do đó có tất cả ![]() trận đấu
trận đấu

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42



Đáp án C
Do thi đấu vòng tròn 1lượt nên 2 đột bất kỳ chỉ đấu với nhau đúng 1 trận. Số trận đấu của giải là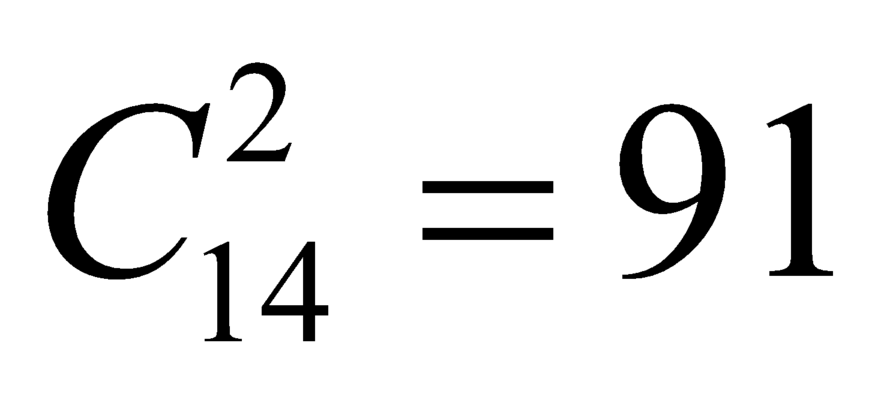
Tổng số điểm của 2 đội trong 1 trận hòa là 2 nên tổng số điểm của 23 trận hòa là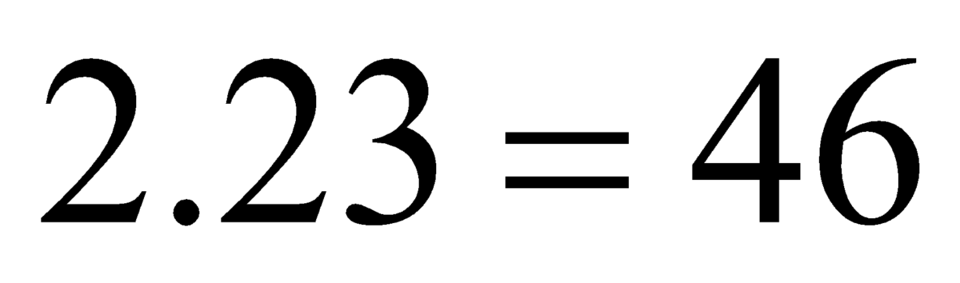
Tổng số điểm của 2 đội trong 1 trận không hòa là 3 nên tổng số điểm của 68 trận không hòa là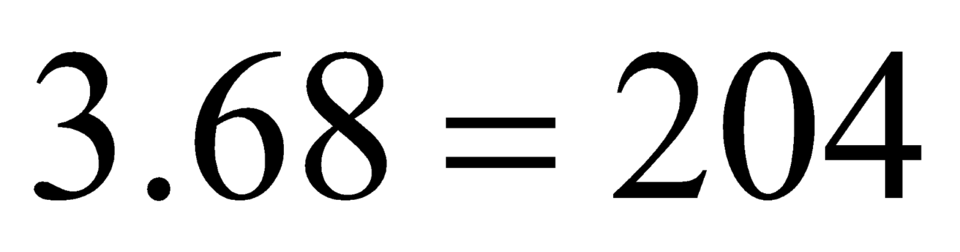
Vậy số điểm trung bình của 1 trận là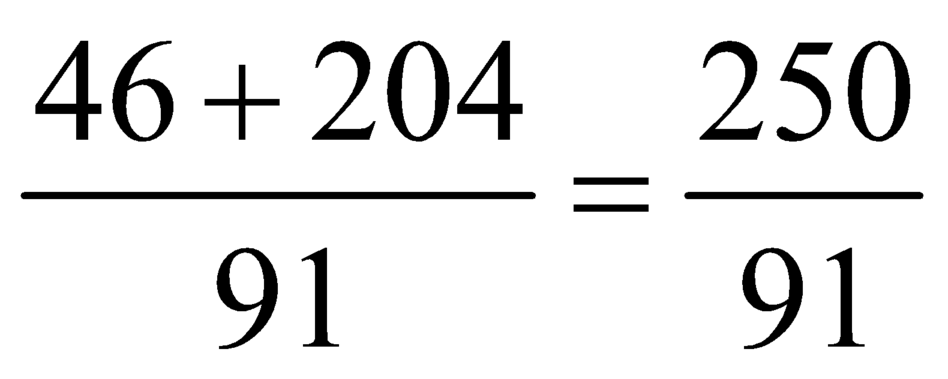 (điểm)
(điểm)