Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

.png)
a) Xét tứ giác DMEA có 3 góc vuông nên DMEA là hình chữ nhật.
Theo tính chất hình chữ nhật thì AM = DE.
b) Do DMEA là hình chữ nhật nên DE giao AM tại trung điểm mỗi đường. Do đó, I cũng là trung điểm AM.
Gọi K, H lần lượt là trung điểm của AB và AC.
Xét tam giác BAM có K, I lần lượt là trung điểm của AB và AM nên KI là đường trung bình.
Vậy IK// BC. Tương tự IH//BC.
Lại có KE//BC nên I thuộc KH.
Do KH cố định nên ta có: Khi M di chuyển trên đoạn BC thì I di chuyển trên đoạn KH.
c) Ta đã có DE = AM nên DE ngắn nhất khi và chỉ khi AM có độ dài ngắn nhất.
Lại có AM là đường xiên nên luôn luôn lớn hơn hoặc bằng đường cao AH.
Vậy thì AM có độ dài ngắn nhất khi AM trung với AH tức là M trùng H.
Tóm lại DE có độ dài ngắn nhất khi M là chân đường vuông góc hạ từ A xuống BC.

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath

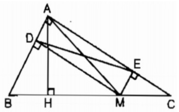
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC

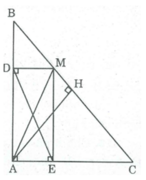
Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
Do đó, AM ≥ AH ( quan hệ đường vuông góc và đường xiên )(dấu " = " xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật .
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE ≥ AH
Vậy DE có độ dài nhỏ nhất là AH khi và chỉ khi điểm M là trung điểm của BC.

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
hihihihihihiihiihiihihiihihihihihihihihihihihihihihiihihiihihihihihihiihihihihihihihihihihihihihihihihhihihihihihihihhiihihihihihiihihiihihihihihihihihihihihihihihihihiihihihihihiihihihihihihihihihiihihihihiihiihihihihiihihihihihiihihihihihiihhiihihihiihihihihihiihihihihhiihhiihiihihihihihihihihihihihiihhiiihhiihhiihihihihihihihiihihih

a) Xét tứ giác AEMF có
\(\widehat{AFM}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{FAE}=90^0\)(gt)
Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AM=EF(Hai đường chéo của hình chữ nhật AFME)
b) Gọi O là giao điểm của AM và EF
Ta có: AMFE là hình chữ nhật(cmt)
nên Hai đường chéo AM và EF cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)
mà O là giao điểm của AM và EF(gt)
nên O là trung điểm của AM; O là trung điểm của EF
Ta có: ΔAHM vuông tại H(gt)
mà HO là đường trung tuyến ứng với cạnh huyền AM(O là trung điểm của AM)
nên \(HO=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà AM=EF(cmt)
nên \(HO=\dfrac{EF}{2}\)
Xét ΔHFE có
HO là đường trung tuyến ứng với cạnh EF(O là trung điểm của EF)
\(HO=\dfrac{EF}{2}\)(cmt)
Do đó: ΔHFE vuông tại H(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)

a,Ta có :
\(AH\perp BC\left(GT\right)\Rightarrow\widehat{HAB}+\widehat{B}=90^o\)
Mà \(\widehat{B}+\widehat{C=90^o}\)( Trong tam giác vuông 2 góc nhọn phụ nhau )
\(\Rightarrow\widehat{HAB}=\widehat{C}\left(1\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\)có :
AM là trung tuyến ứng với cạnh huyền BC ( GT )
\(\Rightarrow AM=MC=\frac{1}{2}BC\)( Tính chất )
Vì \(AM=MC\)
\(\Rightarrow\Delta AMC\)cân tại M ( Định nghĩa )
\(\Rightarrow\widehat{MAC}=\widehat{C}\)( Tính chất ) \(\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\widehat{HAB}=\widehat{MAC}\left(DPCM\right)\)

MDA = DAE = AEM = 90
=> ADME là hcn
Tam giác ABC vuông cân tại A
=> ACB = ABC = 45
mà MEC = 90
=> Tam giác EMC vuông cân tại E
=> EM = EC
mà DM = AE (ADME là hcn)
=> EM + DM = EC + AE = AC = 4 (cm)
PADME = 2 . (EM + DM) = 2 . 4 = 8 (cm)
DE = AM (ADME là hcn)
=> DE nhỏ nhất
<=> AM nhỏ nhất
<=> AM _I_ BC tại M
mà tam giác ABC vuông cân tại A
=> AM là đường trung tuyến
=> M là trung điểm
Vậy DE nhỏ nhất <=> M là trung điểm của BC.

Xét tứ giác ADME, ta có:
∠ A = 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (MDA ) = 90 0
ME ⊥ AC (gt)
⇒ ∠ (MEA ) = 90 0
Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)
⇒ AM = DE ( tính chất hình chữ nhật)