Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Giá trị 5 xuất hiện nhiều lần nhất trong mẫu số liệu (3 lần)
⇒ M 0 = 5

Cách 1. Ta có: Khi cộng vào mỗi số liệu của một dãy số liệu thống kê cùng một hằng số thì phương sai và độ lệch chuẩn không thay đổi. Do đó độ lệch chuẩn của dãy (2) vẫn là 2 kg.
Cách 2. Tính trực tiếp độ lệch chuẩn của dãy (2).
Đáp án: A.

• Ta có:
- Số trung bình cộng x = 55,82 trường là không có nghĩa.
- Trong các số liệu thống kê đã cho có sự chênh lệch quá lớn (điều này chứng tỏ các số liệu thống kê đã cho là không cùng loại)
Chỉ cần một trong hai điều kể trên là đủ để suy ra rằng: Không chọn được số trung bình cộng làm đại diện cho các số liệu thống kê.
• Dễ thấy: Bảng số liệu thống kê đã cho không có mốt.
• Trong trường hợp đã cho, ta chọn số trung vị M e = 40 (trường) để làm đại diện cho các số liệu thống kê đã cho (về quy mô và độ lớn).
Đáp án: B

Chọn A.
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.

*) Sắp xếp thứ tự của mẫu số liệu theo thứ tự không giảm ta được: 1 2 4 5 9 10 11
a) Số trung bình cộng của mẫu số liệu trên là: \(\overline x = \frac{{1{\rm{ + }}2{\rm{ + }}4{\rm{ + }}5{\rm{ + }}9{\rm{ + }}10{\rm{ + }}11}}{7} = 6\)
b) Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 5\)
c) Tứ phân vị của mẫu số liệu trên là:
Trung vị của dãy 1, 2, 4 là: \({Q_1} = 2\)
Trung vị của dãy 9, 10, 11 là: \({Q_3} = 10\)
Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 2\), \({Q_2} = 5\), \({Q_3} = 10\)
d) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 11 - 1 = 10\)
e) Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 10 - 2 = 8\)
g) Phương sai của mẫu số liệu trên là: \({s^2} = \frac{{\left[ {{{\left( {1 - \overline x } \right)}^2} + {{\left( {2 - \overline x } \right)}^2} + ... + {{\left( {11 - \overline x } \right)}^2}} \right]}}{7} = \frac{{96}}{7}\)
h) Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} = \sqrt {\frac{{96}}{7}} \)

Đáp án D.
+ Trung bình cộng của dãy là x ¯ = 7
+ Phương sai của dãy số liệu thống kê là:
S 2 = 1 5 - 7 2 + 1 . 6 - 7 2 + 1 . 7 - 7 2 + 1 . 8 - 7 2 + 1 . 5 5 S 2 = 10 5 = 2

Dựa vào bảng tần số, ta thấy tần số lớn nhất là 47 ứng với cỡ áo 39. Vậy mốt của mẫu số liệu là 39.

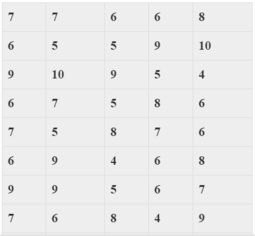

Đáp án B.
Sắp thứ tự các số liệu thống kê thành một dãy không giảm là:
1 4 4 6 7 9 10
Vậy số trung vị là M e = 6
Chú ý: Cách tìm số trung vị M e = 6
+ Sắp thứ tự các số liệu thống kê thành 1 dãy không giảm (không tăng).
+ Nếu số phần tử lẻ thì M e = 6 là số đứng giữa dãy.
+ Nếu số phần tử chẵn thì M e = 6 là trung bình cộng của 2 số đứng giữa dãy.