Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

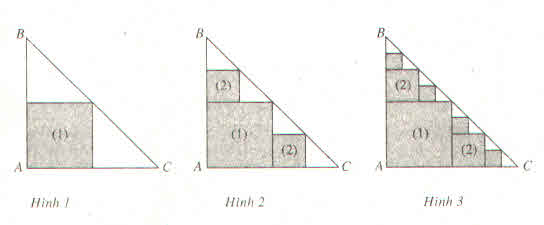
a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .

bn ơi K thuộc SD hả ? ... nếu vậy thì MK sẽ không thể song song với mặt phẳng ( SBC) đâu nhé :)

A B C D M N P Q
a/ Trong mp (BCD) dựng đường thẳng // với CD cắt BD tại P => CD//NP (1)
=> mp (MNP) là mp \(\alpha\)
Trong mp (ACD) từ M dựng đường thẳng //CD cắt AC tại Q => CD//MQ (2)
Từ (1) và (2) => NP//MQ => MPNQ là thiết diện của tứ diện ABCD với mp \(\alpha\)
b/
Xét tg ACD có
MQ//CD và MA=MD => QA=QC (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại của tam giác => MQ là đường trung bình của tg ACD \(\Rightarrow MQ=\frac{CD}{2}\)
Ta có MQ//NP để MPNQ là hình bình hành thì \(MQ=NP=\frac{CD}{2}\) (tứ giác có 1 cặp cạnh đối // và = nhau thì tứ giác là hbh)
=> NP là đường trung bình của tg BCD => N là trung điểm của BC


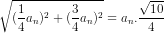 với n ε N*.
với n ε N*. 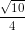








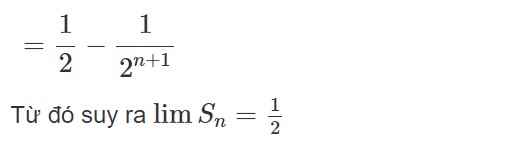
Chọn A.
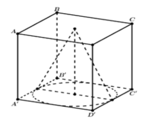
Lời giải. Ta có bán kính hình nón r= a 2 , đường cao h=a,
Diện tích toàn phần