Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}+\overrightarrow{MC}\right|\\ \Rightarrow\left(\overrightarrow{MA}+\overrightarrow{MB}\right)^2-\left(\overrightarrow{MA}+\overrightarrow{MC}\right)^2=0\\ \Rightarrow\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MA}+\overrightarrow{MC}\right)\left(\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MA}-\overrightarrow{MC}\right)=0\\ \Rightarrow\left(2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\left(\overrightarrow{MB}-\overrightarrow{MC}\right)=0\)
Gọi I là trung điểm BC
\(\Rightarrow\left(2\overrightarrow{MA}+2\overrightarrow{MI}\right)\cdot\overrightarrow{CB}=0\\ \Rightarrow\left[{}\begin{matrix}\overrightarrow{CB}=0\\2\overrightarrow{MA}+2\overrightarrow{MI}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}C\equiv B\\\overrightarrow{MA}=-\overrightarrow{MI}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}C\equiv B\\M\text{ là trung điểm }AI\end{matrix}\right.\)
Vậy với \(C\equiv B\) thì M tùy ý
Với \(C\ne B\) thì M là trung điểm đường trung tuyến ứng với BC của \(\Delta ABC\)

\(\text{a) }\left|2\overrightarrow{MA}+3\overrightarrow{MB}\right|=\left|3\overrightarrow{MB}-2\overrightarrow{MC}\right|\\ \Rightarrow\left(2\overrightarrow{MA}+3\overrightarrow{MB}\right)^2=\left(3\overrightarrow{MB}-2\overrightarrow{MC}\right)^2\\ \Rightarrow\left(2\overrightarrow{MA}+3\overrightarrow{MB}\right)^2-\left(3\overrightarrow{MB}-2\overrightarrow{MC}\right)^2=0\\ \Rightarrow\left(2\overrightarrow{MA}+3\overrightarrow{MB}-3\overrightarrow{MB}+2\overrightarrow{MC}\right)\left(2\overrightarrow{MA}+3\overrightarrow{MB}+3\overrightarrow{MB}-2\overrightarrow{MC}\right)=0\\ \Rightarrow\left(2\overrightarrow{MA}+2\overrightarrow{MC}\right)\left[2\left(\overrightarrow{MA}-\overrightarrow{MC}\right)+6\overrightarrow{MB}\right]=0\\ \Rightarrow\left(\overrightarrow{MA}+\overrightarrow{MC}\right)\left(\overrightarrow{CA}+3\overrightarrow{MB}\right)=0\\ \Rightarrow\left[{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MC}=0\\\overrightarrow{CA}+3\overrightarrow{MB}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\overrightarrow{MA}=-\overrightarrow{MC}\\\overrightarrow{CA}=-3\overrightarrow{MB}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}M;A;C\text{ thẳng hàng };M\text{ nằm giữa }A;C\\MA=MC\end{matrix}\right.\\\left\{{}\begin{matrix}CA//MB\\CA=3MB\end{matrix}\right.\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}M\text{ là trung điểm }AC\\CA//MB;CA=3MB\end{matrix}\right.\)
Vậy......
\(b\text{) }\left|4\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|\\ \Rightarrow\left(4\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)^2=\left(2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right)^2\\ \Rightarrow\left(4\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)^2-\left(2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right)^2=0\\ \Rightarrow\left(4\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\left(4\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right)=0\\ \Rightarrow\left(2\overrightarrow{MA}+2\overrightarrow{MB}+2\overrightarrow{MC}\right)\cdot6\overrightarrow{MA}=0\\ \Rightarrow\overrightarrow{MA}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)=0\\ \Rightarrow\left[{}\begin{matrix}\overrightarrow{MA}=0\\\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}M\equiv A\\M\text{ là trọng tâm }\Delta ABC\end{matrix}\right.\)Vậy...........

a) \(MA^2+MB^2=MC^2\)
\(\Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {x - 4} \right)^2} + {\left( {y + 2} \right)^2}\)
\(\Leftrightarrow {x^2} + {y^2} + 12x - 10y - 5 = 0\)
\(\Leftrightarrow {\left( {x + 6} \right)^2} + {\left( {y - 5} \right)^2} = 66\)
Vậy tập hợp các điểm M là một đường tròn.
b) Tâm là điểm (-6 ; 5) bán kính bằng \(\sqrt{66}\)

Gọi I là điểm thỏa mãn:
\(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{IA}+\overrightarrow{IB}+2\left(\overrightarrow{IB}-\overrightarrow{IC}\right)=\overrightarrow{0}\)
Với H là trung điểm AB:
\(2\overrightarrow{IH}+2\overrightarrow{CB}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{IH}=\overrightarrow{BC}\)
Khi đó: \(\left|2\overrightarrow{MI}+\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}\right|=\left|\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MA}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow2\left|\overrightarrow{MI}\right|=\left|\overrightarrow{BA}+\overrightarrow{CA}\right|\)(K là trung điểm BC)
\(\Leftrightarrow2MI=2KA\) \(\Leftrightarrow MI=KA\)
Quỹ tích M là tập hợp các điểm nằm trên đường tròn tâm I bán kính AK.

D nha bạn
Ta có AC=-2AB
AC=MC-MA
AB=-2(MB-MA)
<=>MC-MA=-2(MB-MA)
<=>MC-MA=-2MB+2MA
<=>MC+2MB=MA+2MA
=3MA
Vậy chọn D
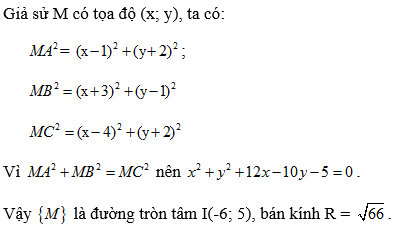
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.