Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(6!\)
Xếp 3 quyẻn Toán cạnh nhau: \(3!\) cách
Xếp 3 quyển Lý cạnh nhau: \(3!\) cách
Hoán vị 2 bộ toán và lý: \(2!\) cách
Xác suất: \(P=\dfrac{3!.3!.2!}{6!}=\dfrac{1}{10}\)

Chọn A
|
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
| 1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
Gọi Ω là biến cố “xếp quyển sách lên kệ sách một cách tùy ý”
=> n( Ω ) = 14!
A là biến cố “xếp 14 cuốn sách lên kệ sách sao cho hai cuốn sách cùng môn không ở cạnh nhau”.
- Xếp quyển sách Tiếng Anh vào kệ có 7! cách.
- quyển sách Tiếng Anh tạo ra 8 chỗ trống (gồm 6 chỗ trống ở giữa và 2 chỗ trống trước sau).
Đánh số từ 1 đến 8, từ trái sang phải cho các chỗ trống. Khi đó ta xét các trường hợp:
TH1: Xếp sách Văn hoặc Toán vào vị trí từ 1 đến 7 có 7! cách.
TH2: Xếp sách Văn hoặc Toán vào vị trí từ 2 đến 8 có 7! cách.
TH3: Xếp cặp sách Văn – Toán chung vào ngăn, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại. Ta có:
+ Số cách chọn cặp sách Văn – Toán: 3.4 cách.
+ Vị trí 2 cuốn sách trong cặp sách: 2! cách.
+ Xếp các sách còn lại vào các ngăn 3,4,5,6,7 có 5! cách
Vậy ta có số cách xếp 1 cặp sách Văn – Toán chung vào ngăn 2, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại là 3.4.2!.5! cách.
Tương tự cho xếp cặp sách Văn – Toán lần lượt vào các ngăn 3,4,5,6,7
Số trường hợp thuận lợi của biến cố là ![]()
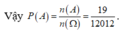

Để sắp xếp số sách đó lên kệ và thỏa mãn đầu bài ta cần làm hai công việc sau:
Đầu tiên; đặt 3 nhóm sách ( toán; văn; anh) lên kệ có 3!=6 cách.
Sau đó; trong mỗi nhóm ta có thể thay đổi cách xếp các quyển sách với nhau:
Nhóm toán có 4!=24 cách.
Nhóm văn có 2!=2 cách.
Nhóm anh có 6!=720 cách.
Theo quy tắc nhân có : 6.24.2.720=207360 cách.
Chọn B.

Số cách chọn 3 quyển sách văn là \(C^3_4=4\).
Số cách chọn 3 quyển sách anh là \(C^3_5=10\).
a, Số cách sắp xếp vào 1 kệ dài là \(9!.4.10=14515200\) cách.
b, Coi số sách mỗi loại là một phần tử.
Số cách sắp xếp thỏa mãn yêu cầu bài toán là \(3!.4.10=240\) cách.

a) Số cách xếp 5 quyển Toán nằm cạnh nhau là: `5! . 10!`
b)
Xếp 5 quyển sách Toán, ta có `5!` cách xếp, mỗi cách xếp đều cho tar 6 khe trống.
`->` Cần xếp 3 quyển Hóa vào 6 khe trống đó.
`->` Số cách xếp là: `5!.`\(A_6^3\)`=14400`.

Chọn D
Tổng có 3 + 4 + 5 = 12 quyển sách được sắp xếp lên một giá sách có 3 ngăn (có 2 vách ngăn). Vì vậy, ta coi 2 vách ngăn này như 2 quyển sách giống nhau. Vậy số phần tử không gian mẫu ![]()
Gọi A là biến cố : “ Sắp xếp các 12 quyển sách lên giá sao cho không có bất kỳ hai quyển sách toán nào đứng cạnh nhau”.
+) Xếp 9 quyển sách ( lý và hóa) cùng 2 vách ngăn có 11 ! 2 ! cách
+) Lúc này, có 12 “khoảng trống” ( do 9 quyển sách ( lý và hóa) cùng 2 vách ngăn tạo ra) để xếp 3 quyển sách toán vào sao cho mỗi quyển vào một “khoảng trống” có A 12 3 cách.
Vậy có tất cả
11
!
2
!
.
A
12
3
cách. Suy ra 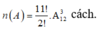
Vậy xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau là:
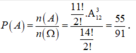

Chọn D
Giá có 3 ngăn như vậy có 2 vách ngăn, coi 2 vách ngăn này là 2 quyển sách giống nhau. Khi đó
bài toán trở thành xếp 14 quyển sách (2 quyển “VÁCH NGĂN” giống nhau) vào 14 vị trí. Đầu
tiên chọn 2 vị trị trí xếp vách ngăn là C 14 2 , 12 vị trí còn lại xếp 12 quyển sách là 12!. Vậy không gian mẫu là C 14 2 .12!.
Gọi A là biến cố “không có bất kì hai quyển sách toán nào đứng cạnh nhau”. Ta tìm số cách xếp thỏa mãn A
Đầu tiên ta xếp 11 quyển sách gồm 4 quyển lí, 5 quyển hóa và 2 quyển “VÁCH NGĂN”. Cũng
như trên, ta chọn 2 vị trí xếp 2 quyển “VÁCH NGĂN” trước là C 11 2 sau đó xếp 9 quyển còn lại là 9!. Vậy số cách xếp 11 quyển này là C 11 2 .9!. Sau khi xếp xong 11 quyển này thì sẽ có sẽ có 12 khe. Ta chọn 3 khe để xếp 3 quyển toán còn lại, là A 12 3 .
Vậy số cách thỏa mãn biến cố A là . C 11 2 .9!. A 12 3
Vậy  .
.
Chọn C
Số cách xếp 9 quyển sách lên một kệ sách dài là 9! . Suy ra số phần tử không gian mẫu: n ( Ω ) = 9!
Gọi A là biến cố: “các quyển sách cùng một môn nằm cạnh nhau”.
Ta xếp các cuốn sách cùng một bộ môn thành một nhóm
Trước hết ta xếp 2 nhóm lên kệ sách chúng ta có: 2! cách xếp
Với mỗi cách xếp 2 nhóm đó lên kệ ta có 5! cách hoán vị các cuốn sách Toán và 4! cách hoán vị các cuốn sách Văn. Suy ra n(A) = 5!.4!.2!
Xác suất cần tìm là