Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:Không áp dụng tính phân phối:
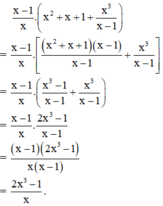
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC
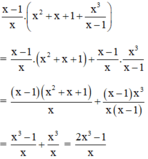

Cách 1 \(\dfrac{x-1}{x}.\left(x^2+x+1+\dfrac{x^3}{x-1}\right)\\ =\dfrac{x-1}{x}.\left(\dfrac{\left(x-1\right)(x^2+x+1)+x^3}{x-1}\right)\\ =\dfrac{x-1}{x}.\dfrac{2x^3-1}{x-1}=\dfrac{2x^3-1}{x}\)
Cách 2 \(\dfrac{x-1}{x}.\left(x^2+x+1+\dfrac{x^3}{x-1}\right)\\ =\dfrac{x-1}{x}.\left(x^2+x+1\right)+\dfrac{x-1}{x}.\dfrac{x^3}{x-1}\\ =\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x}+x^2\\ =\dfrac{x^3-1}{x}+x^2=\dfrac{2x^3-1}{x}\)

\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #

-
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
- Chứng Tỏ Rằng J Hả Bạn ??????




a: \(x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2\)
=100
b: \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\)
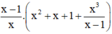
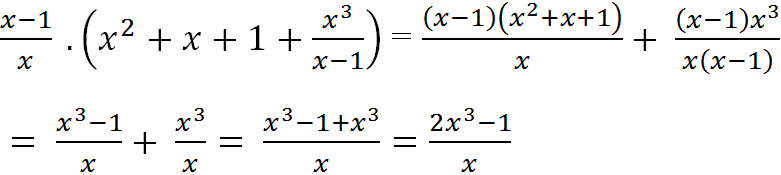

 xy – 1 với đa thức x3 – 2x – 6.
xy – 1 với đa thức x3 – 2x – 6.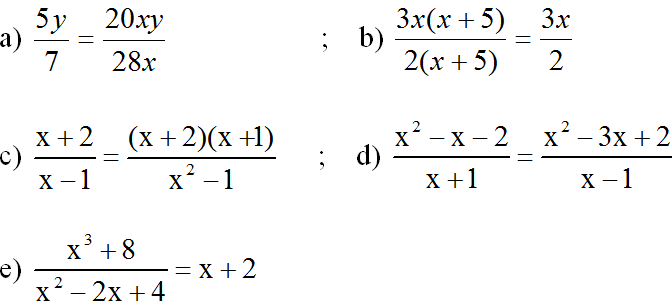

Cách 1:Không áp dụng tính phân phối:
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC