Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).


a) π < a < => sina < 0, cosa < 0, tana > 0
sin2a = 2sinacosa = 2(-0,6)(-) = 0,96
cos2a = cos2 a – sin2 a = 1 – 2sin2 a = 1 - 0,72 = 0,28
tan2a = ≈ 3,1286
b) < a < π => sina > 0, cosa < 0
sina =
sin2a = 2sinacosa = 2.
cos2a = 2cos2a - 1 = 2 - 1 = -
tan2a =
c) < a < π =>
< 2a < 2π => sin2a < 0, cos2a > 0, tan2a < 0
sin2a = - 1 = -0,75
cos2a =
tan2a = -

a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ; ).
Ta có : y’ = - 1 ≥ 0, x ∈ [0 ;
); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ;
).
Từ đó ∀x ∈ (0 ; ) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.
b) Xét hàm số y = g(x) = tanx – x - . với x ∈ [0 ;
).
Ta có : y’ = - 1 - x2 = 1 + tan2x - 1 - x2 = tan2x - x2
= (tanx - x)(tanx + x), ∀x ∈ [0 ; ).
Vì ∀x ∈ [0 ; ) nên tanx + x ≥ 0 và tanx - x >0 (theo câu a).
Do đó y' ≥ 0, ∀x ∈ [0 ; ).
Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; ). Từ đó : ∀x ∈ [0 ;
) thì g(x) > g(0) ⇔ tanx – x -
> tan0 - 0 - 0 = 0 hay tanx > x +
.

a) Hoành độ điểm P là :
xp = OP = OM. cos α = R.cosα
Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:
b) Đặt t = cosα => t ∈ . (vì α ∈
), α = arccos t.
Ta có :
V' = 0 ⇔
hoặc (loại).
Ta có bảng biến thiên:
Từ đó suy ra V(t) lớn nhất ⇔ , khi đó :
.

a) + cos2250 = cos(1800 + 450 ) = -cos450 =
+ sin2400 = sin(1800 + 600 ) = -sin600 =
+ cot(-150 ) = -cot150 = -tan750 = -tan(300 + 450 )
= -2 - √3
+ tan 750 = cot150= 2 + √3
b)
+ sin = sin
= sin
cos
+ cos
sin
+ cos = cos
= cos
cos
+ sin
sin
+ tan = tan(π +
) = tan
= tan
=
= 2 - √3

Tập xác định : D = R. y' = => y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
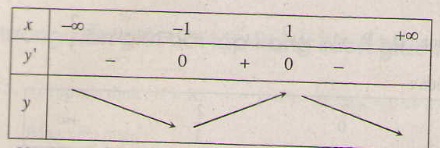
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).

Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
Bảng biến thiên :
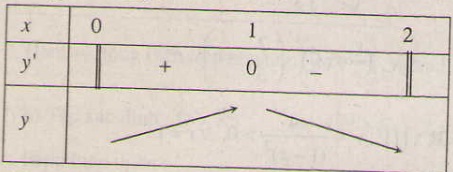
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).
HD: Đường tròn đã cho có phương trình x2 + y2 = 8
Từ đó ta có: y = ±
Gọi S là diện tích phần tô xám ở hình bên :
và
Vậy .
.
c47a4970.html#ixzz43P4gPVRT
Chép y chang cách giải SGK mà chẳng giải thích gì thêm?