Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Tại t: dao động thứ hai có vận tốc là:
− 20 π 3 c m / s = − V 2 max 2 . 3 cm/s
và tốc độ đang giảm nên tại t pha dao động thứ 2 là 2π/3 rad.
Mà x1 và x2 lệch pha nhau π/3 suy ra tại t thì pha của x1 là π/3.
Suy ra A 1 = 3.2 = 6 cm.
A = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ = 6 2 + 10 2 + 2.6.10. cos π 3 = 14 c m
Suy ra khi pha dao động tổng hợp là − 2 π 3 thì li độ dao động tổng hợp là:
x = A . cos − 2 π 3 = − 7 c m .

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Đáp án B
Phương pháp: Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng phương, cùng tần số
Cách giải:
Ta có x = x1 + x2 => x2 = x – x1
x = 3cos(πt - 5π/6) (cm)
x1 = 5cos(πt + π/6) (cm) => - x1 = 5cos(πt - 5π/6)
=> x2 = 8cos(πt - 5π/6) (cm) => Chọn B

- Có thể bấm nhanh bằng máy tính:
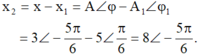
- Vậy dao động thứ 2 có phương trình li độ:
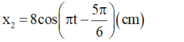

Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

Đáp án D
Phương pháp: Sử dụng̣ giản đồ Fresnen
Cách giải:
x1 + x2 = x => x1 +6 = 9cm => x1 = 3cm
Dựa vào đề bài ta biểu diễn được các vecto dao động như hình bên:
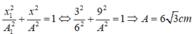
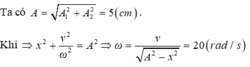
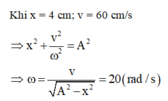
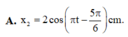
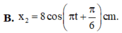
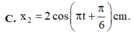
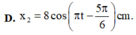
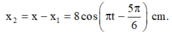
Đáp án D