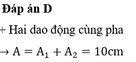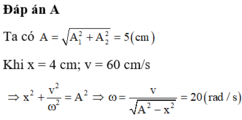Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dao động tổng hợp x = x1 + x2
+ Khi x2 = 0 thì x1 = x - x2 = \(-5\sqrt{3}\)
+ Khi x1 = - 5 thì x2 = x - x1 = -2 + 5 = 3
Giả sử pt \(x_1=10\cos\left(\omega t\right)\) thì \(x_2=A_2\cos\left(\omega t+\varphi\right)\) (với \(\left|\varphi\right|<\frac{\pi}{2}\))
Theo giả thiết ta có:
\(\begin{cases}10\cos\left(\omega t\right)=-5\sqrt{3}\\A_2\cos\left(\omega t+\varphi\right)=0\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t\right)=-\frac{\sqrt{3}}{2}\\\cos\left(\omega t+\varphi\right)=0\end{cases}\)
cos O M1 M2 -√3/2 60°
Do \(\left|\varphi\right|<\frac{\pi}{2}\) nên ta chỉ có trường hợp như hình trên thỏa mãn, nghĩa là ta tìm đc \(\varphi=-\frac{\pi}{3}\)
Mặt khác: \(\begin{cases}10\cos\left(\omega t'\right)=-5\\A_2\cos\left(\omega t'+\varphi\right)=3\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t'\right)=-\frac{1}{2}\\\cos\left(\omega t'+\varphi\right)=\frac{3}{A_2}\end{cases}\)
Cũng biểu diễn trên đường tròn lượng giác như trên, ta được
cos O M1 M2 -1/2 1/2
\(\Rightarrow A_2=6cm\)
Biên độ tổng hợp:
\(A^2=10^2+6^2+2.10.6.\cos\frac{\pi}{3}\Rightarrow A=14\)cm.
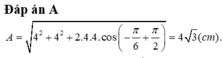
Chọn đáp án A.
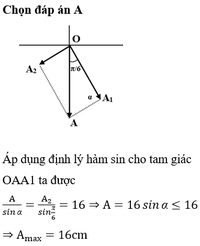
Biên độ tổng hợp của hai dao động là lớn nhất khi hai dao động cùng pha với nhau
⇒ α = 0 ( r a d )
=> Hai dao động vuông pha → α = 0,5π