Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
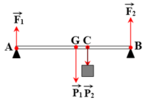
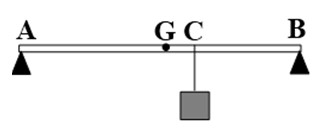
Phân tích các lực tác dụng lên thanh AB như hình.
→ F1 + F2 = P1 + P2 = 150 (1)
Gọi d1, d2 khoảng cách từ các lực , tới vị trí trọng tâm mới của vật: d1 + d2 = 10 cm (1)
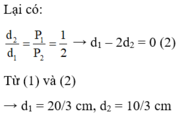
→ Khoảng cách từ các lực , đến trọng tâm mới của vật là
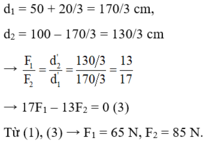

Chọn B.
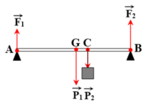
Phân tích các lực tác dụng lên thanh AB như hình.
→ F 1 + F 2 = P 1 + P 2 = 150 (1)
Gọi d 1 , d 2 khoảng cách từ các lực P 1 ⇀ , P 2 ⇀ tới vị trí trọng tâm mới của vật: d 1 + d 2 = 10 cm (1)
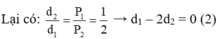
Từ (1) và (2) → d 1 = 20/3 cm, d 2 = 10/3 cm
→ Khoảng cách từ các lực F ⇀ 1 , F 2 ⇀ đến trọng tâm mới của vật là
d 1 = 50 + 20/3 = 170/3 cm
d 2 = 100 – 170/3 = 130/3 cm
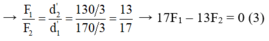
Từ (1), (3) → F 1 = 65 N, F 2 = 85 N.

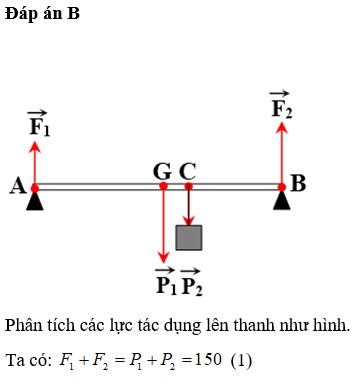
Đáp án B
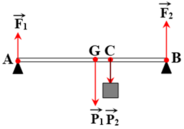
Phân tích các lực tác dụng lên thanh AB như hình.
→ F1 + F2 = P1 + P2 = 150 (1)
Gọi d1, d2 khoảng cách từ các lực P 1 ⇀ , P 2 ⇀ tới vị trí trọng tâm mới của vật: d1 + d2 = 10 cm (1)
Lại có: d 2 d 1 = P 1 p 2 = 1 2 → d1 – 2d2 = 0 (2)
Từ (1) và (2) → d1 = 20/3 cm, d2 = 10/3 cm
→ Khoảng cách từ các lực F 1 → , F 2 → đến trọng tâm mới của vật là
d1 = 50 + 20/3 = 170/3 cm, d2 = 100 – 170/3 = 130/3 cm
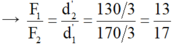
→ 17F1 – 13F2 = 0 (3)
Từ (1), (3) → F1 = 65 N, F2 = 85 N.

Chọn B.
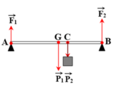
Phân tích các lực tác dụng lên thanh AB như hình.
→ F1 + F2 = P1 + P2 = 150 (1)
Gọi d1, d2 khoảng cách từ các lực , tới vị trí trọng tâm mới của vật: d1 + d2 = 10 cm (1)
![]()
Từ (1) và (2) → d1 = 20/3 cm, d2 = 10/3 cm
→ Khoảng cách từ các lực , đến trọng tâm mới của vật là
d1 = 50 + 20/3 = 170/3 cm, d2 = 100 – 170/3 = 130/3 cm
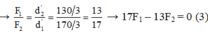
Từ (1), (3) → F1 = 65 N, F2 = 85 N.

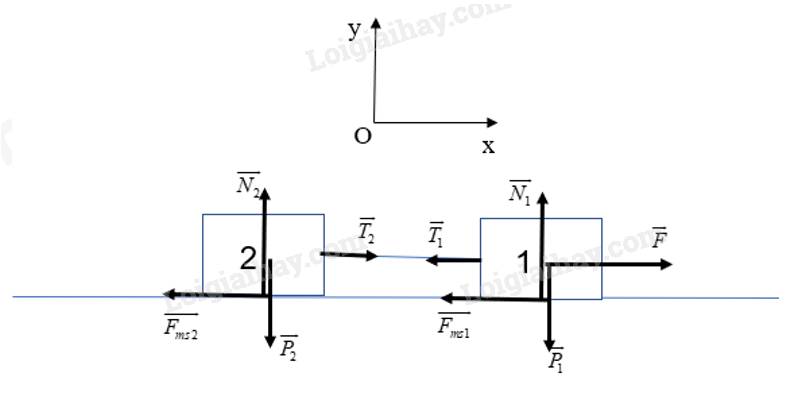
Chọn hệ quy chiếu như hình vẽ:
Theo định luật 2 Newton cho hệ vật, ta có:
\(\overrightarrow {{P_1}} + \overrightarrow {{P_2}} + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{F_{ms2}}} + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = ({m_1} + {m_2}).\overrightarrow a \) (1)
Chiếu (1) lên Ox, ta có
\(\begin{array}{l}F - {F_{ms1}} - {F_{ms2}} - {T_1} + {T_2} = ({m_1} + {m_2}).a\\ \Leftrightarrow F - \mu ({N_1} + {N_2}) = ({m_1} + {m_2}).a\end{array}\)
\( \Leftrightarrow a = \frac{{F - \mu ({N_1} + {N_2})}}{{{m_1} + {m_2}}}\) (2)
(do \({T_1} = {T_2}\))
Chiếu (1) lên Oy, ta có:
\(\begin{array}{l}{N_1} + {N_2} - {P_1} - {P_2} = 0\\ \Leftrightarrow {N_1} + {N_2} = {P_1} + {P_2}\\ \Leftrightarrow {N_1} + {N_2} = ({m_1} + {m_2}).g\end{array}\)
Thay \({N_1} + {N_2} = ({m_1} + {m_2}).g\) vào (2), ta có:
\(\begin{array}{l}a = \frac{{F - \mu .g({m_1} + {m_2})}}{{{m_1} + {m_2}}}\\ \Leftrightarrow a = \frac{{45 - 0,2.9,8.(5 + 10)}}{{5 + 10}}\\ \Leftrightarrow a = 1,04(m/{s^2})\end{array}\)
Xét vật 1
Theo định luật 2 Newton, ta có
\(\overrightarrow {{P_1}} + \overrightarrow {{N_1}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{T_1}} = {m_1}.\overrightarrow a \) (3)
Chiếu (3) lên Ox, có
\(\begin{array}{l}F - {F_{ms1}} - {T_1} = {m_1}.a\\ \Leftrightarrow {T_1} = F - \mu {N_1} - {m_1}.a\end{array}\)
Chiếu (3) lên Oy, ta có \({N_1} = {P_1} = {m_1}.g\)
\(\begin{array}{l} \Rightarrow {T_1} = F - \mu {m_1}g - {m_1}.a\\ \Leftrightarrow {T_1} = 45 - 0,2.5.9,8 - 5.1,04\\ \Leftrightarrow {T_1} = 30(N)\end{array}\)
Vậy gia tốc của hai vật là 1,04 m/s2 và lực căng của dây nối là 30 N.

Ta có :
Trọng lực của thanh đặt ở trung điểm thanh (gọi G là trung điểm thanh AB)
Ta giải bài toán trong trường hợp tổng,
Áp dụng quy tắc momen trục quay tại B:
\(mg.BGsin\alpha=F.BA\)
\(\rightarrow F=mg\frac{BGsin\alpha}{BA}=50.10\frac{sin\alpha}{2}=250sin\alpha\)
Phản lực của tường phải cân bằng với F và P.
Phản lực theo phương ngang: \(N_x=F.sin\alpha\)
Phản lực theo phương thẳng đứng:\(N_y=mg-F.cos\alpha\)
Gọi góc hợp giữa phản lực và phương ngang là \(\phi\)
\(tan\phi=\frac{Ny}{Nx}=\frac{mg-Fcos\alpha}{Fsin\alpha}\)
\(=\frac{500-250sin\alpha.cosalpha}{250sinalpha^2}=\frac{2-sin\alpha.cosalpha}{sinalpha^2}\)
Độ lớn của phản lực:
\(N=\sqrt{N_x^2+N^2_y}=\sqrt{F^2+m^2g^2-2mgFcosalpha}\)
Trong 2 trường hợp góc α này chúng ta thay số và tìm các giá trị cần tìm

chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F
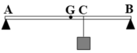

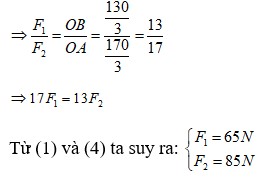
Chọn B.
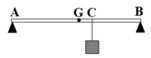
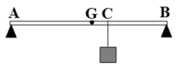
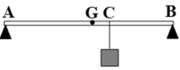
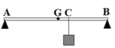
Phân tích các lực tác dụng lên thanh AB như hình.
→ F1 + F2 = P1 + P2 = 150 (1)
Gọi d1, d2 khoảng cách từ các lực P 1 → , P 2 → tới vị trí trọng tâm mới của vật: d1 + d2 = 10 cm (1)
Từ (1) và (2) → d1 = 20/3 cm, d2 = 10/3 cm
→ Khoảng cách từ các lực , đến trọng tâm mới của vật là
d1 = 50 + 20/3 = 170/3 cm, d2 = 100 – 170/3 = 130/3 cm
Từ (1), (3) → F1 = 65 N, F2 = 85 N.