Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi n là số năm cần gửi, suy ra 100 1 + 7 % n ≥ 250 ⇔ n ≥ 13,54 ⇒ n = 14

Đáp án A
Phương pháp:
Công thức lãi kép: T = M 1 + r n với:
T là số tiền cả vốn lẫn lãi sau n kì hạn;M là số tiền gửi ban đầu; n là số kỳ hạn; r là lãi suất định kỳ, tính theo %.
Cách giải: Gọi n là số năm cần gửi ít nhất để người đó có 250 triệu.
Ta có: 250.10 6 = 100.10 6 1 + 7 , 4 n
⇔ n = log 1 + 7 , 4 % 250.10 6 100.10 6 ≈ 12 , 8 ⇒ n = 13 (năm).
Chú ý khi giải: HS sẽ phân vân khi chọn số năm cần gửi ít nhất vì n ~ 12 , 8 nên có thể sẽ chọn đáp án sai là n=12.

Đáp án A
Số tiền lãi người này nhận được sau 5 năm là
50 ( 1 + 0 , 07 ) 5 - 50 ≈ 20 , 128 (triệu đồng).

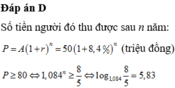
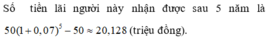

Đáp án C
Theo công thức lãi kép ta có T = A 1 + r n trong đó
T là cả tiền gốc lẫn lãi khi lấy về
A là số tiền ban đầu
R là lãi suất
N là số kỳ hạn
Khi đó 250 = 100 1 + 7 100 n ⇒ n = log 1 , 07 250 100 ≈ 13 , 54 năm.
Để người đó lãnh được số tiền 250 triệu thì người đó cần gửi trong khoảng thời gian 14 năm