Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

@phạm hồng lê: Bạn giải chi tiết giúp mình hoặc chỉ cho mình hướng làm được không?

Đáp án: A
HD Giải: Áp dụng quy tắc bàn tay trái ta xác định được hướng của lực từ tác dụng lên mỗi cạnh của khung dây như hình vẽ.
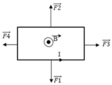
- Lực từ tác dụng lên mỗi cạnh l1 = 30 cm: ![]()
- Lực từ tác dụng lên mỗi cạnh l2 = 20cm: ![]()
Lực từ tổng hợp tác dụng lên khung dây: ![]()

a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(

Đáp án: A
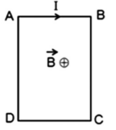
Áp dụng định lý hàm số cosin trong tam giác ABC ta tính được B C = 20 3 c m
Cường độ dòng điện chạy trong các cạnh của khung dây là:
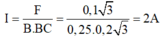

1/
a/ \(E_c=NS\left|\frac{\Delta B}{\Delta t}\right|.\cos60^0=10.20.10^{-4}.\frac{1}{2}.\left|\frac{-0,04}{0,01}\right|=0,04\left(V\right)\)
b/ \(I=\frac{E_c}{R}=\frac{0,04}{0,2}=0,2\left(A\right)\)
2/ \(F_t=2.10^{-7}.\frac{I_1I_2}{r}.l=2.10^{-7}.\frac{2.1}{0,2}.0,4=8\left(N\right)\)

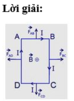
Các lực từ tác dụng lên từng cạnh AB,CD của khung dây có điểm đặt tại trung điểm của mỗi cạnh, có phương nằm trong mặt phẵng chứa khung dây và vuông góc với từng cạnh, có chiều như hình vẽ và có độ lớn: F A B = F C D = B . I . A B = 0 , 02.5.0 , 05 = 5.10 − 3 N
Đáp án cần chọn là: C

Từ thông cực đại: \(\phi_0=N.B.S = 2000.10^{-2}.0,2^2=0,8Wb\)
t = 0 chọn lúc mặt phẳng khung dây vuông góc với đường sức, có nghĩa véc tơ pháp tuyến của khung trùng với đường sức
\(\Rightarrow \varphi =0\)
Vậy biểu thức từ thông: \(\phi=0,8.\cos(100\pi t)(Wb)\)

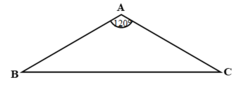
Áp dụng công thức F = Bilsin α ( với α = π /2, sin α =1) và quy tắc bàn tay trái để xác định độ lớn và hướng của lực từ tác dụng lên mỗi cạnh của khung dây dẫn(Hình 19-20.2G). Từ đó, ta suy ra :
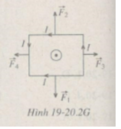
- Lực từ tác dụng lên mỗi cạnh l 1 = 30 cm :
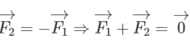
Có độ lớn F 1 = F 2 = BI l 1 = 0,10.5,0.0,30 = 0,15N.
- Lực từ tác dụng lên mỗi cạnh l 2 = 20 cm :
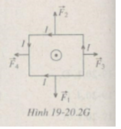
Có độ lớn F 3 = F 4 = Bi l 2 = 0,10.5,0.0,20 = 0,10N.
Chọn C
Gỉa sử từ trường hướng từ trong ra ngoài mặt phẳng hình vẽ, theo quy tắc bàn tay trái hướng cùa lực từ tác dụng lên các cạnh giống như hình vẽ.
Vì các cạnh vuông góc với từ trường nên α = 90 độ, độ lớn lực từ tính theo:
F = B I l sin α = B I l ⇒ F 1 = F 3 = 0 , 1.5.0 , 3 = 0 , 15 N F 2 = F 4 = 0 , 1.5.0 , 2 = 0 , 1 N ⇒ F 1 + 2 F 2 + 3 F 3 + 4 F 4 = 1 , 2 N