Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D

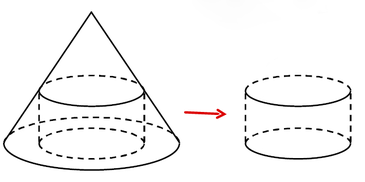
Xét mặt cắt và lấy các điểm như hình vẽ bên cạnh.
Theo đề thì O A = O B = r = 30 cm và O H = h = 120 cm
Đặt O C = O D = R là bán kính đường tròn đáy của khúc gỗ khối trụ thì:
E C O H = A C O A = O A − O C O A ⇔ E C h = r − R R ⇔ E C = 4 30 − R
Thể tích khúc gỗ khối trụ là
V = π R 2 . E C = 4 π . R 2 . 30 − R ⇒ f R = 30 R 2 − R 3
Xét hàm số f R trên 0 ; 30 ⇒ max f R = 4000
Vậy thể tích lớn nhất của khối trụ V = 0 , 016 m 3

Cây gỗ sẽ được cưa thành 5 khúc, như vậy có tất cả 4 lần cưa. Mỗi lần cưa hết 5 phút và bác nghỉ thêm 3 phút, như vậy tổng số thời gian 1 lần cưa là 8 phút. Vậy thời gian bác cưa hết cây gỗ là 8 x 4 = 32 (phút)
Trong lời giải của bạn Duyên, phải trừ đi 3 phút lần nghỉ cuối cùng không tính, còn 32 - 3 = 29 phút

Cây gỗ sẽ được cưa thành 5 khúc, như vậy có tất cả 4 lần cưa. Mỗi lần cưa hết 5 phút và bác nghỉ thêm 3 phút, như vậy tổng số thời gian 1 lần cưa là 8 phút.
Vậy thời gian bác cưa hết cây gỗ là:
8 x 4 = 32 (phút)
Phải trừ đi 3 phút lần nghỉ cuối cùng không tính, còn
32 - 3 = 29 phút
ĐS: 29 phút

Đổi 8m=80dm
Số lần cưa là:80:16=5(lần)
Mỗi lần cưa nghỉ thêm 3 phút nên 1 lần cưa tất cả 8 phút
Vậy mất số phút là:
5x8=40(phút)
Đổi: 8m = 80dm
Số lần cưa cây gỗ là:
80 : 16 = 5 (lần)
Thời gian cưa hết cây gỗ là:
5 x 5 = 25 (phút)
Từ lần cưa 1 đến 2, lần 2 đến 3, ..., lần 4 đến 5, ta có tất cả 4 lần cưa
=> Thời gian nghỉ của bác thợ mộc là:
3 x 4 = 12 (phút)
Bác thợ mộc cưa xong cây gỗ hết số thời gian là:
25 + 12 = 37 (phút)
Đáp số: 37 phút.
Tick mk nha! ![]()

Đáp án A
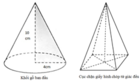
Chu vi đường tròn C = 2 π r ⇒ 2 π r = 14 c m ⇒ r = 7 c m
Xét khối món có thể tích V = 1 3 π r 2 h = 343 3 π c m 3 ⇒ h = 7 c m
Khối cầu được almf từ khối nón có bán kính mặt cầu lớn nhất khi khối cầu nội tiếp khối nón
Khi đó bán kính khối cầu (S) là R S = r . h r + r 2 + h 2 = 7 − 1 + 2 c m
Vậy diện tích lớn nhất cần tính là:
S = 4 π R 2 = 196 π 3 − 2 2 c m 2

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra



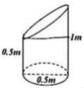

Đáp án D
Gọi r 0 ; h 0 lần lượt là bán kính đáy và chiều cao của khối trụ.
Theo giả thuyết, ta có:
r 0 r = h − h 0 h ⇔ r 0 = 30. 120 − h 0 120 = 30 − h 0 4
Suy ra thể tích khối trụ là:
V = π r 0 2 . h 0 = π 30 − h 0 4 2 . h 0 = π . 120 − h 0 2 . h 0 16
Xét hàm số f t = t 120 − t 2 với t ∈ 0 ; 120 suy ra: max 0 ; 120 f t = 256000
Vậy thể tích lớn nhất của khối trụ là:
V max = π 256000 16 . 1 100 3 = 0 , 016 π c m 3