Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Gọi T là khoảng thời gian mà một nửa số hạt nhân của hỗn hợp hai đồng vị bị phân rã (chu kỳ bán rã của hỗn hợp).
Sau thời gian t 1 số hạt nhân của hỗn hợp còn lại:
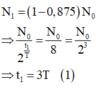
Sau thời gian t 2 số hạt nhân của hòn hợp còn lại:

Đáp án C

Số hạt nhân chưa bị phân rã (số hạt nhân còn lại)
\(N= N_0 2^{-\frac{t}{T}} = N_02^{-\frac{0,5T}{T}}= N_02^{-0,5}= \frac{N_0}{\sqrt{2}}.\)

Đáp án: A.
Gọi T là khoảng thời gian mà một nửa số hạt nhân của hỗn hợp hai đồng vị bị phân rã (chu kỳ bán rã của hỗn hợp, ta có thể tính được T = 5,277 ngày).
Sau thời gian t1 số hạt nhân của hỗn hợp còn lại ![]() (*)
(*)
Sau thời gian t2 số hạt nhân của hỗn hợp còn lại ![]() (**).
(**).
Từ (*) và (**) suy ra t1/t2 = 3/2 hay t1 = 1,5t2

Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)

lập tỉ số \(\frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\) =7 tính được t=3T
thời điểm t2=t1+26.7=3T+26.7
lập tỉ số như trên thay t2=3T+26.7 vào tính được T=8.9
Chọn B