Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đội A:
+) Số trung bình: \(\overline x = \frac{{28 + 24 + 26 + 25 + 25 + 23 + 20 + 29 + 21 + 24 + 24}}{{11}} = 24,45\)
+) Mốt: \({M_o} = 24\)
+) Phương sai \({S^2} = \frac{1}{{11}}\left( {{{28}^2} + {{24}^2} + ... + {{24}^2}} \right) - 24,{45^2} = 6,65\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 2,58\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 20, 21, 23, 24, 24, 24, 25, 25, 26, 28, 29
\({Q_2} = {M_e} = 24\)
\({Q_1}\) là trung vị của nửa số liệu: 20, 21, 23, 24, 24. Do đó \({Q_1} = 23\)
\({Q_3}\) là trung vị của nửa số liệu: 25, 25, 26, 28, 29. Do đó \({Q_3} = 26\)
Đội B:
+) Số trung bình: \(\overline x = \frac{{32 + 20 + 19 + 21 + 28 + 29 + 21 + 22 + 29 + 19 + 29}}{{11}} = 24,45\)
+) Mốt: \({M_o} = 29\)
+) Phương sai \({S^2} = \frac{1}{{11}}\left( {{{32}^2} + {{20}^2} + ... + {{29}^2}} \right) - 24,{45^2} = 22,12\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 4,7\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 19, 19, 20, 21, 21, 22, 28, 29, 29, 29, 32.
\({Q_2} = {M_e} = 22\)
\({Q_1}\) là trung vị của nửa số liệu: 19, 19, 20, 21, 21. Do đó \({Q_1} = 20\)
\({Q_3}\) là trung vị của nửa số liệu: 28, 29, 29, 29, 32. Do đó \({Q_3} = 29\)
b)
Ta so sánh độ lệch chuẩn \(2,58 < 4,7\) do dó đội A có độ tuổi đồng đều hơn.
Chú ý
Ta không so sánh số trung vị vì không có giá trị nào quá lớn hay quá nhỏ so với các giá trị còn lại.

\(h\left( x \right) = - 0,1{x^2} + x - 1\) có \(\Delta = \frac{3}{5} > 0\), có hai nghiệm phân biệt là \({x_1} = 5 - \sqrt {15} ;{x_2} = 5 + \sqrt {15} \)
Ta có bảng xét dấu như sau
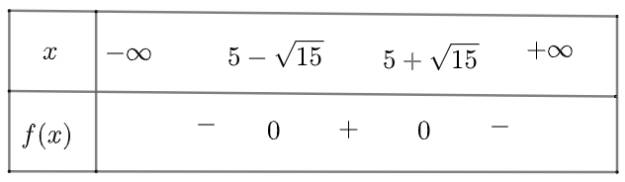
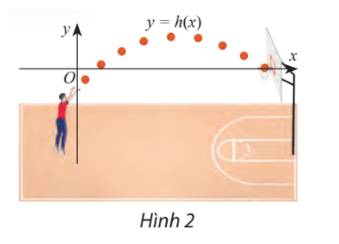
Vậy khoảng bóng nằm trên vành rổ là \(x \in \left( {1,2;8,9} \right)\)mét
khoảng bóng nằm dưới vành rổ là \(x \in \left( { - \infty ;1,2} \right) \cup \left( {8,9; + \infty } \right)\) mét
khoảng bóng nằm ngang vành rổ là \(x \simeq \left\{ {1,2;8,9} \right\}\)

Danh sách những môn thi đấu mà cả hai trường đã đề xuất là: Bóng bàn, Bóng đá, Bóng rổ, Cầu lông.
bài;1 món thịt kho
hà rất muốn ăn món thịt kho tàu do mẹ nấu.
khi có thời gian, hà và mẹ đi chợ mua ít thịt về
nấu
bài;2;tìm đoạn van vừa đọc.
khi có thời gian,hà và mẹ đi đâu
A,đi chợ Bđi về quê C đi chơi

Bài 1:
Giải:
Vì 2 số chẵn liên tiếp hơn kém nhau 2 đơn vị nên số chẵn bé kém hơn số chẵn lớn 2 đơn vị.
Số chẵn bé là :
( 86 - 2 ) : 2 = 42
Số chẵn lớn là:
86 - 42 = 44
Đáp số: số chẵn bé: 42
số chẵn lớn: 44
Bài 2:
Giải:
Tổng số tuổi của các thành viên trong đội bóng đó là:
11 x 22 = 242 ( tuổi )
Nếu không tính thủ môn thì tổng số tuổi của các thành viên còn lại là:
21 x 10 = 210 ( tuổi )
Tuổi của thủ môn là:
242 - 210 = 32 ( tuổi )
Đáp số: 32 tuổi
1
trung bình cộng 2 số chẵn đó là:
86:2=43
vậy số lớn là 43+1=44
số bé là 43-1=42
2
tổng số tuổi của thủ môn và các cầu thủ là:
22x11=242(tuổi)
tổng số tuổi của 10 cầu thủ là:
10x22=220(tuổi)
tuổi của thủ môn là:
242-220=24(tuổi)
3
a)luợng mật ong còn ở trại là:
135.62,5%=

Mỗi cách chọn ra và xếp thứ tự 5 cầu thủ đá luân lưu từ đội bóng có 11 cầu thủ là một chỉnh hợp chập 5 của 11.
Vậy ta có \(A_{11}^5 = 55440\) (cách chọn ra và xếp thứ tự 5 cầu thủ đá luân lưu từ đội bóng có 11 cầu thủ)

a) Chú ý rằng với hai người \(A\)và \(B\)thi đấu với nhau thì \(A\)thi đấu với \(B\)và \(B\)thi đấu với \(A\).
Mỗi người sẽ đấu với \(n-1\)người, nên tổng số ván đấu của giải là:
\(\frac{n\left(n-1\right)}{2}\).
b) Giả sử \(n=12\).
Tổng số ván đấu của giải là: \(\frac{12.11}{2}=66\).
Tổng số điểm của tất cả các kì thủ là: \(2\times66=132\).
Kì thủ cuối thắng ba kì thủ đứng đầu, do đó số điểm kì thủ cuối ít nhất là \(2.3=6\).
Do số điểm các kì thủ đôi một khác nhau nên tổng số điểm tối thiểu của tất cả các kì thủ là:
\(6+7+8+9+10+11+12+13+14+15+16+17=138>132\).
Do đó không thể xảy ra điều này.
Ta có đpcm.

Số bàn thắng trung bình trong mỗi trận đấu được tính bằng tổng cộng số bàn thắng của tất cả các trận đấu rồi chia cho số trận đấu.
Số bàn thắng trung bình trong mỗi trận đấu \( = \frac{{6 + 6 + 2 + 1 + 2 + 4 + 3}}{7} = 3,43\)

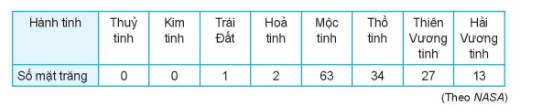
a) Sắp xếp lại số liệu:
0 0 1 2 13 27 34 63
Trung vị là \(\dfrac{(2+13)}{2}=7,5.\)
Ta không chọn số trung bình vì số trung bình là 17,5 chênh lệch với 63 lớn. Mốt cũng thế.
b) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.
Số đường truyền trung bình là: \(\dfrac{{32 + 24 + 20 + 14 + 23}}{5} = 22,6\)
c) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.
IQ trung bình là \(\frac{{80 + {\kern 1pt} 102 + {\kern 1pt} 83 + {\kern 1pt} 103 + {\kern 1pt} 108 + {\kern 1pt} 94 + {\kern 1pt} 110 + {\kern 1pt} 106 + {\kern 1pt} 104 + {\kern 1pt} 100}}{{10}} = 99\)
d) Ta thấy có hai giá trị 42 chênh lệch lớn với các số còn lại nên ta chọn Mốt để đo xu thế trung tâm.
Mốt là 15 (tần số là 3).
Chú ý
Mẫu dữ liệu có sự chênh lệch quá lớn thì không nên chọn số trung bình để đo xu thế trung tâm.

Đáp án A