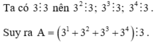
Không thực hiện phép tính, chứng minh rằng A = 3 1...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

15 tháng 2 2017

Không thực hiện phép tính, chứng minh rằng A = 3 1 + 3 2 + 3 3 + 3 4 chia hết cho 3.

#Toán lớp 6

Cao Minh Tâm

15 tháng 2 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NimoTVLinhPéow

29 tháng 1 2019 - olm

Chứng minh rằng A chia hết cho 3 trong phép tính sau:

2+2²+2³+2⁴+2⁵+2⁶+2⁷+2⁸

PHÉP TÍNH TRÊN CÓ CHIA HẾT KHÔNG CHO 3 ?VÌ SAO?

#Toán lớp 6

shitbo

29 tháng 1 2019

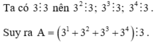
Cái này số nhỏ nên tớ tính luôn nhé :)

A=2+2^2+2^3+......+2^8

=> 2A=2^2+2^3+.......+2^9

=> 2A-A=A=2^9-2=512-2=510 chia hết cho 3(đpcm)

Đúng(0)

Hoàng Ninh

29 tháng 1 2019

Đặt \(A=2+2^2+2^3+2^4+2^5+2^6+2^7+2^8\)

\(\Rightarrow2A=2^2+2^3+2^4+2^5+2^6+2^7+2^8+2^9\)

\(\Rightarrow2A-A=\left(2^2+2^3+2^4+2^5+2^6+2^7+2^8+2^9\right)-\left(2+2^2+2^3+2^4+2^5+2^6+2^7+2^8\right)\)

\(\Rightarrow A=2^9-2\)

\(\Rightarrow A=512-2=510⋮3\)

Vậy A chia hết cho 3 (đpcm)

Đúng(0)

Thuy Tran

3 tháng 10 2016 - olm

Bài 1:Chứng tỏ rằng:

a)Tổng của 3 số tự nhiên liên tiếp là một số chia hết cho 3

b)Tổng của 4 số tự nhiên liên tiếp là một số không chia hết cho 4

Bài 2:Không thực hiện phép tính,xét xem mỗi tổng,hiệu sau có chia hết cho 2 không?vì sao?

a)357-207

b)3689+425-1540

c)24a+10b+11 (với a,b∈∈ N)

#Toán lớp 6

Trần Phương Thảo

3 tháng 10 2016

Bài 1:Chứng tỏ rằng:

a)Tổng của 3 số tự nhiên liên tiếp là một số chia hết cho 3

b)Tổng của 4 số tự nhiên liên tiếp là một số không chia hết cho 4

Bài 2:Không thực hiện phép tính,xét xem mỗi tổng,hiệu sau có chia hết cho 2 không?vì sao?

a)357-207

b)3689+425-1540

c)24a+10b+11 (với a,b\(\in\) N)

#Toán lớp 6

Lightning Farron

3 tháng 10 2016

Bài 1:

a)Gọi 3 số đó là a;a+1;a+2

Ta có:

a+a+1+a+2=(a+a+a)+(1+2)

=3a+3=3(a+1) chia hết 3

Vậy ta có tổng của 3 số tự nhiên liên tiếp là một số chia hết cho 3

b)Gọi 4 số đó là a;a+1;a+2;a+3

Ta có:

a+a+1+a+2+a+3=(a+a+a+a)+(1+2+3)

=4a+6

Ta thấy: 4a chia hết 4, mà 6 không chia hết 4

Vậy ta có tổng của 4 số tự nhiên liên tiếp là một số không chia hết cho 4

Đúng(0)

Hà My Trần

3 tháng 10 2015 - olm

Giúp mình tí đi ♥♥
Bài 1 : Tìm 2 chữ số tận cùng :( Trình bày rõ hộ mình nha )
a, \(3729^{543}\)
b, \(829^{145}\)
Bài 2 : Chứng tỏ rằng tổng của 4 số tự nhiên liên tiếp không chia hết cho 4 , tổng của 4 số tự nhiên chẵn liên tiếp chia hết cho 4
Bài 3 : Cho A = 570 + 345 + 1 . Không thực hiện phép tính xét xem A có chia hết cho 3 , 5 , 10 hay không ?

#Toán lớp 6

Minh Triều

3 tháng 10 2015

Tôi Nghèo Kệ Đời Tôi tìm 2 chữ số lận

Đúng(0)

PHẠM THỊ LINH CHI

10 tháng 11 2016 - olm

BÀI 1;CHO TỔNG A = 270\(+\)3105\(+\)150.KHÔNG THỰC HIỆN PHÉP TÍNH,XÉT XEM TỔNG A CÓ CHIA HẾT CHO 2,3,5,9 KO?TẠI SAO

BÀI 2;ĐIỀN CHỮ SỐ VÀO DẤU * DỂ SỐ 1*5* CHO HẾT CHO 2,3,5,6,9

BÀI 3;Chứng tỏ rằng với mọi số tự nhiên n thì tích (n + 3) (n + 6) chia hết cho 2

đừng nhìn đáp án trong SBT nha

#Toán lớp 6

Hà My Trần

3 tháng 10 2015 - olm

Bài 2 :Chứng tỏ rằng số có dạng abccba bao giờ cũng chia hết cho 11
Bài 1 :Tìm số tự nhiên n nhỏ nhất sao cho khi chia cho 3 , 5 , 7 thì được số dư theo thứ tự là 2 , 3 , 4

Bài 3 : Không thực hiện phép tính xét xem A = 570 + 345 + 1 có chia hết cho 3 , 5 , 10 hay không ?

#Toán lớp 6

Đoàn Phương Linh

25 tháng 12 2017

1. Cho A = \(2^{2016}-1\) . Chứng minh rằng A chia hết cho 105.

2.Chứng minh rằng \(5^{2017}+7^{2015}\) chia hết cho 12.

3. Chứng minh rằng B = \(3^{2^{2n}}+10\) chia hết cho 13.

4. Chứng minh rằng C = \(3^{2^{4n+1}}+2^{3^{4n+1}}+5\) luôn chia hết cho 22.

#Toán lớp 6

Ngô Tấn Đạt

26 tháng 12 2017

1. \(A=2^{2016}-1\)

\(2\equiv-1\left(mod3\right)\\ \Rightarrow2^{2016}\equiv1\left(mod3\right)\\ \Rightarrow2^{2016}-1\equiv0\left(mod3\right)\\ \Rightarrow A⋮3\)

\(2^{2016}=\left(2^4\right)^{504}=16^{504}\)

16 chia 5 dư 1 nên 16^504 chia 5 dư 1

=> 16^504-1 chia hết cho 5

hay A chia hết cho 5

\(2^{2016}-1=\left(2^3\right)^{672}-1=8^{672}-1⋮7\)

lý luận TT trg hợp A chia hết cho 5

(3;5;7)=1 = > A chia hết cho 105

2;3;4 TT ạ !!

Đúng(0)

Nguyễn Minh Quân

24 tháng 3 2021

1.Thực hiện phép tính (1/3 -1)×(1/6 -1)×(1/10 -1)×...×(1/45 -1)2. Cho B=1+ 1/2 +1/3 +...+1/2010 , biết B=phân số m/nChứng minh rằng m chia hết cho 2011.3. Cho P= 2/3 × 4/5 × 6/7 ×...× 98/99.Chứng minh rằng P< 1/7.Giúp mình với!Mình cần gấp

#Toán lớp 6

Nguyễn Lê Phước Thịnh

24 tháng 3 2021

Bài 1:

Ta có: \(\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{6}-1\right)\left(\dfrac{1}{10}-1\right)\cdot...\cdot\left(\dfrac{1}{45}-1\right)\)

\(=\dfrac{-2}{3}\cdot\dfrac{-5}{6}\cdot\dfrac{-9}{10}\cdot...\cdot\dfrac{-44}{45}\)

\(=\dfrac{-2}{3}\cdot\dfrac{-5}{6}\cdot\dfrac{-9}{10}\cdot\dfrac{-14}{15}\cdot\dfrac{-20}{21}\cdot\dfrac{-27}{28}\cdot\dfrac{-35}{36}\cdot\dfrac{-44}{45}\)

\(=\dfrac{11}{27}\)

Đúng(0)