Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C

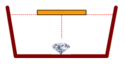
Để người ở ngoài bề không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa của tấm bè bị phản xạ toàn phần, không cho tia khúc xạ ra ngoài không khí.
→ Góc tới giới hạn ứng với cặp môi trường nước và không khí:
![]()
Từ hình vẽ, ta có ![]()
→ Rmin = htanigh = 2,83 m.

Đáp án C
Mắt không thấy đầu A khi tia sáng từ A tới mặt nước tại I (mép miếng gỗ) xảy ra phản xạ toàn phần:
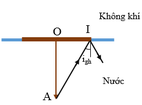
sin i g h = 1 n = 1 1,33 ⇒ i g h = 48,75 o
Ta có i ≥ i g h và R = O A . tan i
→ R min = O A . tan i g h = 2,5. tan 48,75 o ≈ 2,85 m

Chọn đáp án C
Để người ở ngoài bề không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa của tấm bè bị phản xạ toàn phần, không cho tia khúc xạ ra ngoài không khí.

→ Góc tới giới hạn ứng với cặp môi trường nước và không khí: sin i g h = n 2 n 1 = 3 4
Từ hình vẽ, ta có tan i g h = R min h → R m i n = h tan i g h = 2 , 83 m

Đáp án B
Để người ở ngoài bể không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa của bể bị phản xạ toàn phần, không cho tia khúc xạ ra ngoài không khí
→ Góc tới giới hạn ứng với cặp môi trường nước và không khí:
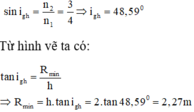

H S I i i gh 20cm
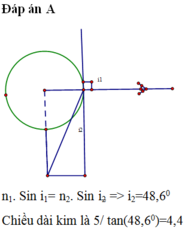
Để mắt người quan sát ở mặt nước không thấy vật sáng ở đáy chậu thì không có tia sáng nào từ vật S thoát ra ngoài, như vậy ít nhất tia tới SI cho tia khúc xạ là là mặt nước như hình vẽ, khi đó góc \(i=i_{gh}\)
=> \(\sin i = \sin i_{gh}=\frac{1}{n}=\frac{3}{4}\)
=>\(\tan i = \frac{3}{\sqrt 7}\)
Mà \(\tan i = \frac{HI}{HS}\Rightarrow HS = HI/\tan i = 20/\frac{3}{\sqrt 7}=\frac{20\sqrt 7}{3}\)cm.
Vậy chiều sâu của nước trong chậu là HS = \(\frac{20\sqrt 7}{3}\)cm.




Đáp án C
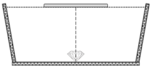
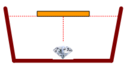
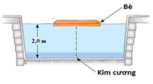
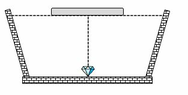
+ Để người ở ngoài bề không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa của tấm bè bị phản xạ toàn phần, không cho tia khúc xạ ra ngoài không khí.
Góc tới giới hạn ứng với cặp môi trường nước và không khí:
sin i g h = n 2 n 1 = 3 4
+ Từ hình vẽ, ta có
tan i g h = R min h → R min = h . tan i g h = 2 , 83 m