Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔOAM và ΔOCP có
góc OAM=góc OCP
OA=OC
góc AOM=góc COP
=>ΔOAM=ΔOCP
=>OM=OP
=>O là trung điểm của MP
Xét ΔOQD và ΔONB có
góc ODQ=góc OBN
OD=OB
góc QOD=góc NOB
=>ΔOQD=ΔONB
=>OQ=ON
=>O là trung điểm của QN
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
=>MNPQ là hbh

Nhà hàng Tôm hùm kính chào quý khách ĐC : 255 Nguyễn Huệ, Q tân bình , TP HCM nhà hàng của gđ mik rất mong dc đón các bn

Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành


ABCD là hbh=> AD//BC=> góc DAC= góc ACB và AO=OC
Xét tam giác AOE và tam giác COF ta có
góc AOE = góc COF (2 góc đối xừng)
AO=OC
góc DAC= góc ACB
=> tam giác AOE = tam giác COF=> OE=OF
CHứng minh tương tự ta có tam giác AOK= tam giác COH=> OK=OH
Xét tứ giác EHFK có EH và FK là 2 đường chéo cắt nhau tại O
lại có OE=OF
OH=OK
=> EHFk là hình bình hành (do 2 đường chéo cắt nhau tại trung điểm mỗi đường)
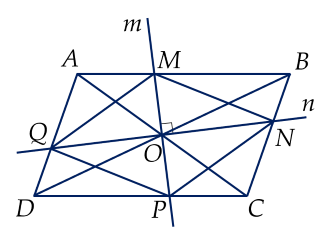
a) ����ABCD là hình bình hành nên hai đường chéo ��,��AC,BD cắt nhau tại �O là trung điểm của mỗi đường.
Xét Δ���ΔOBM và Δ���ΔODP có:
��=��OB=OD ( giả thiết)
���^=���^OBM=ODP (so le trong)
���^=���^BOM=DOP (đối đỉnh)
Vậy Δ���=Δ���ΔOBM=ΔODP (g.c.g)
Suy ra ��=��OM=OP (hai cạnh tương ứng)
Chứng minh tương tự Δ���=Δ���ΔOAQ=ΔOCN (g.c.g) suy ra ��=��OQ=ON (hai cạnh tương ứng)
����MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Hình bình hành ����MNPQ có hai đường chéo ��⊥��MP⊥NQ nên là hình thoi.
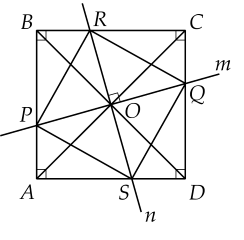
a) ����ABCD là hình bình hành nên hai đường chéo ��,��AC,BD cắt nhau tại �O là trung điểm của mỗi đường.
Xét Δ���ΔOBM và Δ���ΔODP có:
��=��OB=OD ( giả thiết)
���^=���^OBM=ODP (so le trong)
���^=���^BOM=DOP (đối đỉnh)
Vậy Δ���=Δ���ΔOBM=ΔODP (g.c.g)
Suy ra ��=��OM=OP (hai cạnh tương ứng)
Chứng minh tương tự Δ���=Δ���ΔOAQ=ΔOCN (g.c.g) suy ra ��=��OQ=ON (hai cạnh tương ứng)
����MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Hình bình hành ����MNPQ có hai đường chéo ��⊥��MP⊥NQ nên là hình thoi.