Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

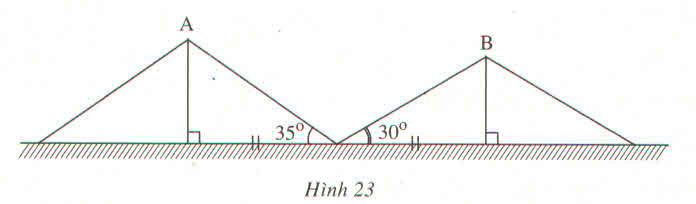
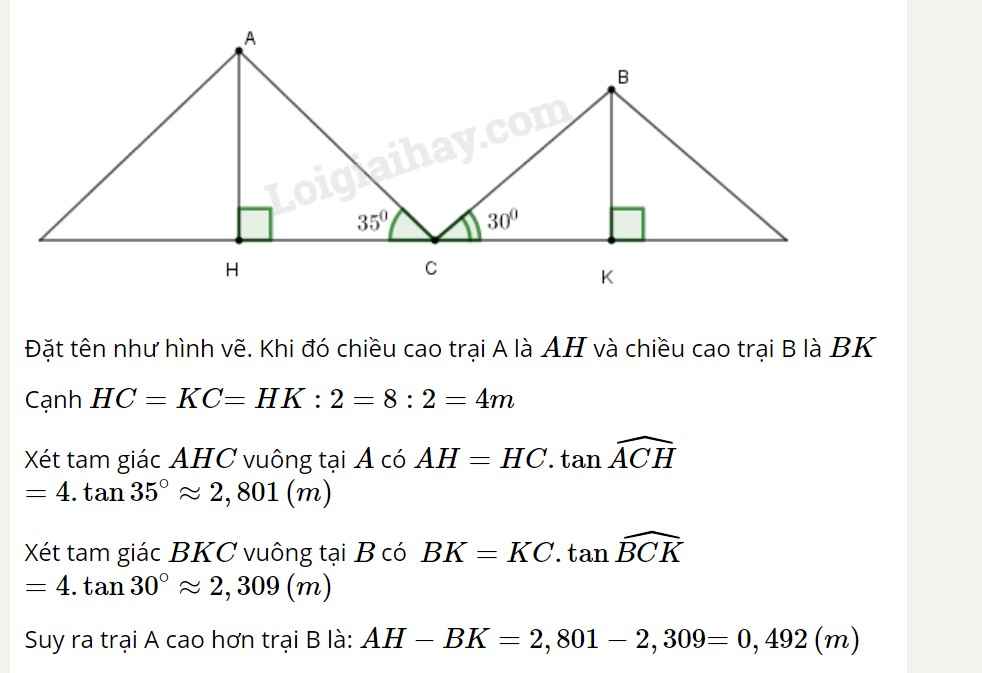
Trong tam giác vuông BIK có:
IB = IK.tg ∠IKB = IK.tg(50o + 15o) = 380.tg 65o ≈ 814 (m)
Trong tam giác vuông AIK có:
IA = IK.tg ∠IKA = IK.tg 50o = 380.tg50o ≈ 452 (m)
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)

a) Khoảng cách giữa 2 vị trí đó là :
\(\frac{20000}{180}.\left(72-42\right)\simeq2800\left(km\right)\)
b) Bán kính của Trái Đất là :
\(\frac{20000}{3,14}\simeq6400\left(km\right)\)
Độ dài đường xích đạo là :
\(20000.2=40000\left(km\right)\)
Vì trái đất là hình cầu :
Thể tích hình cầu được tính dưới dạng : \(V=\frac{4}{3}.3,14.R^3\)( R là bán kính )
Vậy thể tích Trái Đất là :
\(\frac{4}{3}.3,14.\left(6400\right)^3\simeq1097509547000\left(km^3\right)\)

a) ta có : VT = \(\left(\sqrt{3}-1\right)^2=3-2\sqrt{3}+1=4-2\sqrt{3}\) = VP
vậy \(\left(\sqrt{3}-1\right)^2=4-2\sqrt{3}\) (đpcm)
b) ta có : VT = \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}-\sqrt{3}\)
= \(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}\) = \(\left|\sqrt{3}-1\right|-\sqrt{3}\) = \(\sqrt{3}-1-\sqrt{3}\) = 1 = VP
vậy \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=-1\) (đpcm)

Gọi C là vị trí của máy bay.
Kẻ CH⊥ABCH⊥AB
Trong tam giác vuông ACH, ta có:
AH=CH.cotgˆA(1)AH=CH.cotgA^(1)
Trong tam giác vuông BCH, ta có:
BH=CH.cotgˆB(2)BH=CH.cotgB^(2)
Từ (1) và (2) suy ra:
(AH+BH)=CH.cotgˆA+CH.cotgˆB(AH+BH)=CH.cotgA^+CH.cotgB^
Suy ra:
CH=ABcotgˆA+cotgˆB=ABcotg40∘+cotg30∘≈102,606(cm)
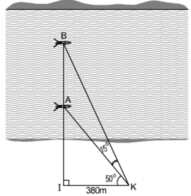
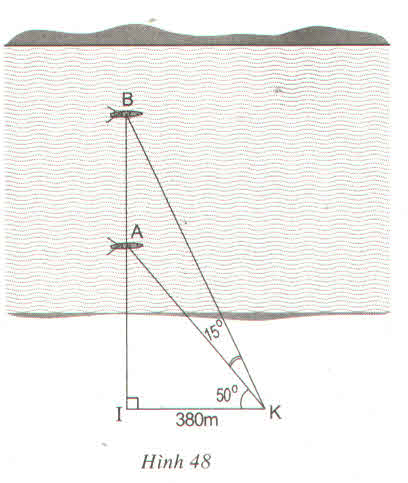

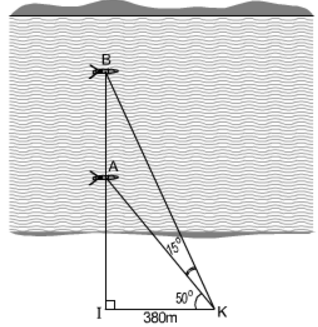
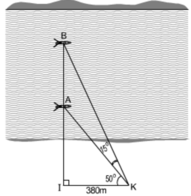
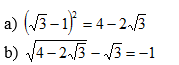


Trong tam giác vuông BIK có:
I B = I K . t g ∠ I K B = I K . t g ( 50 ° + 15 ° ) = 380 . t g 65 ° ≈ 814 ( m )
Trong tam giác vuông AIK có:
I A = I K . t g ∠ I K A = I K . t g 50 ° = 380 . t g 50 ° ≈ 452 ( m )
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)