Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_{0max}\left(\text{∗}\right)\)
+Khi chiếu bức xạ có \(\lambda_1:v_{0max1}=\sqrt{\frac{2\left(\frac{hc}{\lambda_1}-A\right)}{m}}\left(1\right)\)
+Khi chiếu bức xạ có \(\lambda_2:v_{0max2}=\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\left(2\right)\)
Từ \(\text{(∗)}\) ta thấy lhi \(\lambda\) lớn thì \(v_{0max}\) nhỏ
\(\Rightarrow v_{0max1}=2,5v_{0max2}\left(\lambda_1<\lambda_2\right)\)
\(\Leftrightarrow\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}=2,5\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\)
\(\Leftrightarrow\frac{hc}{\lambda_1}-A=6,25\left(\frac{hc}{\lambda_2}-A\right)\) với \(A=\frac{hc}{\lambda_0}\)
\(\Rightarrow\lambda_0=\frac{5,25\lambda_1\lambda_2}{6,25\lambda_1-\lambda_2}=\frac{5,25.0,4.0,6}{6,25.0,4-0.6}=0,663\mu m\)

1) Công thoát của êlectron ra khỏi bề mặt catôt
\(A=\frac{hc}{\lambda_0}=3,025.10^{-19}J\)
2) Vận tốc ban cực đại của electron
\(V_{max}=\sqrt{\frac{2hc}{m}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)}=5,6.10^5m\text{/}s\)
3) Hiệu điện thế hãm để không có electron về catôt.
\(v_h=\frac{hc}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)=0,91V\)

Đáp án C
- Ban đầu:
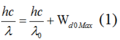
- Sau khi giảm bước sóng kích thích 2 lần:
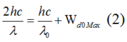
- Vì đối với một kim loại nhất định thì giới hạn quang điện không thay đổi. Thay λ 0 = 2 λ vào (1) và (2) rồi lập tỉ số ta được:
![]()

Đáp án B
+ Ta có λ 1 < λ 2 → ε 1 > ε 2 → v 1 = 1 , 5 v 2 .
+ Áp dụng công thức Einstein về hiệu ứng quang điện cho hai trường hợp ta có:
h c λ 1 = h c λ 0 + E d 1 h c λ 2 = h c λ 0 + E d 2 → h c λ 1 = h c λ 0 + 2 , 25 E d 2 h c λ 2 = h c λ 0 + E d 2 ⇒ 1 , 25 λ 0 = 2 , 25 λ 2 - 1 λ 1
⇔ 1 , 25 λ 0 = 2 , 25 0 , 5 - 1 0 , 4 ⇒ λ 0 = 0 , 625 μ m .

Đáp án A
Số photon chiếu tới:
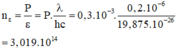
Số electron bứt ra khỏi Catot: 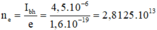
Hiệu suất lượng tử là:
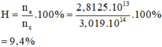
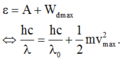
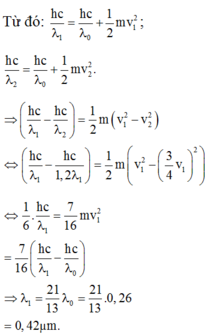


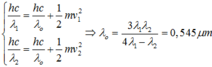
Đáp án A.
Ta có:
= 1 , 7 . 10 - 19 J