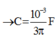Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng giản đồ vecto
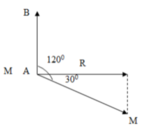
Cách giải:
Có:
Z C R = 1 3 ⇒ R = 3 Z C ⇒ Z L = 4 Z C
⇒ Z C = 30 Ω = 1 ω C ⇒ C = 10 - 3 3 π F

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Ta có Um không đổi và để UAm luôn không đổ vs mọi gtri của R thì : Um=UAm hay ZL=2ZC =2.100=200 → L=2/π ( D)
Sử dụng hình vẽ suy luận cho nhanh : R ZL ZC UAm Um

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Xét đoạn mạch MB có điện áp hiệu dụng gấp đôi điện áp hiệu dung trên R suy ra góc giữa \(U_{MB}\) và \(i\) là \(60^0\)
Mà \(u\) lệch pha \(90^0\) so với \(u_{MB}\)
Suy ra độ lệch pha giữa u và i là \(\varphi =30^0\)
Ta có:
\(P=U. I. \cos \varphi=120\sqrt 3.0,5.\cos30^0=90W\)
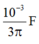
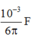
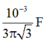
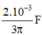


Đáp án A
+ Biểu diễn vectơ các điện áp.
Ta có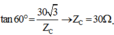 .
.