Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) A T ( 25 ) K(9) M(13) V(24) ( Hình vẽ có thể k chính xác lắm )
b) \(T\subset A\) , \(V\subset A\) , \(K\subset A\)
c) \(T\cap V=M\)
\(T\cap M=M\)
\(V\cap M=M\)
\(K\cap T=\varnothing\)
\(K\cap V=\varnothing\)
d) Số h/sinh của lowsps 6A là : \(25+24-13+9=45\) ( h/s )

Gọi số học sinh khối 7 của trường đó là : b (học sinh)
Gọi số học sinh khối 8 của trường đó là : c (học sinh)
Gọi số học sinh khối 9 của trường đó là : d (học sinh)
Với điều kiện :a>0;b>0;c>;d>0 (*).
Theo đề bài, tổng số học sinh khối 6 và khối 7 chiếm \(\dfrac{25}{44}\) tổng số học sinh toàn trường,nên :
a+b= \(\dfrac{25}{44}\)\(\times\)1320=750 (1)
Số học sinh khối 8 chiếm 25% số học sinh toàn trường nên:
c=25% \(\times\)1320=330 (học sinh)
Số học sinh khối 8 là : d=1320 \(-\)(a+b)\(-\)c
= 1320 \(-\)750 \(-\)330 = 240 (học sinh)
Theo bài ra, tổng số học sinh khối 6 và khối 8 bằng 2 lần số học sinh khối 7 ,nên:
a+c=2b (2)
Từ (1)và (2) ,ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=750\\a+c=2b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-b\\750-b+330=2b\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=750-b\\1080-b=2b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-b\\-b-2b=-1080\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=750-b\\-3b=-1080\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-360=390\\b=360\end{matrix}\right.\)thỏa mản(*)
Vậy khối 6 có 390 (học sinh), khối 7có 360(học sinh), khối 8 có 330 (học sinh), khối 9 có 240 (học sinh).

Gọi số HS của lớp 6E là a. Ta có:
\(\frac{2}{9}a+5=\frac{1}{3}a\Rightarrow5=\frac{1}{3}a-\frac{2}{9}a\)
\(\Rightarrow a\left(\frac{1}{3}-\frac{2}{9}\right)=5\Rightarrow a\left(\frac{3}{9}-\frac{2}{9}\right)=5\)
\(\Rightarrow\frac{1}{9}a=5\Rightarrow a=5:\frac{1}{9}=45\)
=> Số học sinh của lớp 6E là 45 học sinh.
=> Trong kì thi cuối năm lớp 6E có số HS đạt loại giỏi môn Toán là:
\(45\cdot\frac{1}{3}=\frac{45}{3}=15\left(HS\right)\)
- Nếu kh chắc chắn bn có thể thử lại nhé :)

a) Minh họa bằng hình vẽ
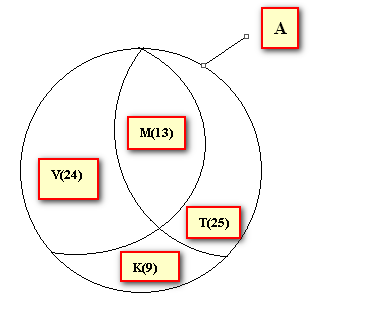
b) T⊂AT⊂A
V⊂AV⊂A
K⊂AK⊂A
c) T∩V=MT∩V=M
T∩M=MT∩M=M
V∩M=MV∩M=M
K∩T=∅K∩T=∅
K∩V=∅K∩V=∅
d) Số học sinh của lớp 6A là:
(24 + 25 – 13) + 9 = 45(học sinh)
dễ lấy... mà bạn học số phẩy chưa zậy?Nếu học rùi thì lấy 25 cộng 24 trừ 13 chia 9 bằng 13 kết quả bằng 13 nhà bạn
chục bạn học zỏi hihihi

Đặt A=\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}\)
A=\(\frac{1}{2\cdot2}+\frac{1}{3\cdot3}+\frac{1}{4\cdot4}+...+\frac{1}{100\cdot100}\)
A<\(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{99\cdot100}\)
A<\(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
A<\(1-\frac{1}{100}=\frac{99}{100}< 1\)
Vậy \(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1\)
Ta có : \(\frac{1}{2^2}< \frac{1}{1.2};\frac{1}{3^2}< \frac{1}{2.3};\frac{1}{4^2}< \frac{1}{3.4};...;\frac{1}{100^2}< \frac{1}{99.100}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
Đặt : \(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(\Rightarrow A=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow A=\frac{1}{1}-\frac{1}{100}=\frac{99}{100}\)
Vì : \(A< 1\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1\)
Vậy ...

Ta có :
\(\begin{cases}\frac{1}{2^2}< \frac{1}{1.2}\\\frac{1}{3^2}< \frac{1}{2.3}\\.....\\\frac{1}{100^2}< \frac{1}{99.100}\end{cases}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+....+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{99.100}\)
Mà \(\frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{99.100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}< 1\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+....+\frac{1}{100^2}< 1\)
Ta có: \(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
\(\frac{1}{4^2}< \frac{1}{3.4}\)
..........................
\(\frac{1}{100^2}=\frac{1}{99.100}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}\)
Vì \(1-\frac{1}{100}< 1\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1\)
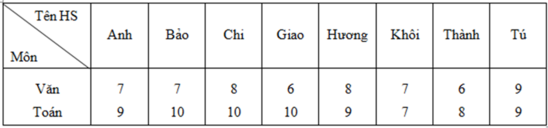






Tập hợp tên các học sinh có tổng số điểm hai môn lớn hơn 16 là:
{Bảo, Chi , Hương, Tú}.