Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Sử dụng giản đồ vecto trong dòng điện xoay chiều
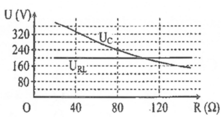
Khi C = C 1 thì điện áp trên hai đầu R không phụ thuộc R, chứng tỏ có cộng hưởng. U R = U AB → Z C 1 = Z L
Khi C = C 2 thì điện áp trên hai đầu R L không phụ thuộc R, chứng tỏ U LR = U AB
Ta có giản đồ vecto
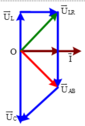
Từ giản đồ thấy được U C 2 = 2 U L
![]()

Đáp án A
Khi L = L 1 → U R = IR = UR R 2 + Z L 1 − Z C 2 = U 1 + Z L 1 − Z C 2 R 2
Để U R không phụ thuộc R thì Z L 1 − Z C = 0 → Z L 1 = Z C *
Khi L = L 2 → U R C = I R 2 + Z C 2 = U R 2 + Z C 2 R 2 + Z L 2 − Z C 2 = U 1 + Z L 2 2 − 2 Z L 2 Z C R 2 + Z C 2
Để U R C không phụ thuộc R thì Z L 2 = 2 Z c * *
Từ (*) và (**) → Z L 2 = 2 Z L 1 → L 2 = 2 L 1

trong trường hợp ban đầu
điện áp R cực đại nên tại f1 xảy ra hiện tượng cộng hưởng
\(Z_L=Z_C\)
\(LC=\frac{1}{\omega^2_1}\)
Trong trường hợp sau thì điện áp AM không đổi khi thay đổi R, lúc cố định tần số nghĩa là cảm kháng và dung kháng đều cố định
như vậy thì chỉ có trường hợp duy nhất là Uam bằng với U
Khi đó
\(Z_{LC}=Z_L=Z_C-Z_L\)
\(Z_C=2Z_L\)
\(LC=\frac{1}{2\omega^2_2}\)
Suy ra
\(\omega^2_1=2\omega^2_2\)
\(f_1=\sqrt{2}f_2\)

Đáp án A.
Ta có:
![]()
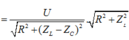
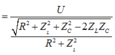
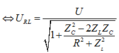
Trên đồ thị ta thấy:
Khi R thay đổi, U R L không đổi nên:
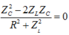
![]()
Khi 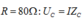
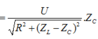
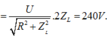
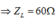 và
và ![]()
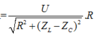
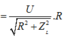


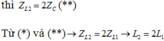


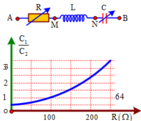

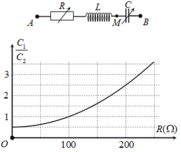

Đáp án B
+ Khi C = C 1 thì điện áp hiệu dụng hai đầu biến trở: U R = I . R = U . R R 2 + Z L − Z C 1 2 = U 1 + Z L − Z C 1 2 R 2
Để U R không phụ thuộc vào R thì: Z L − Z C 1 = 0 ⇒ Z C 1 = Z L 1
+ Khi C = C 2 thì điện áp hiệu dung hai đầu đoạn mạch chứa L và R:
U LR = I . R 2 + Z L 2 = U . R 2 + Z L 2 R 2 + Z L 2 − 2 Z L Z C 2 + Z C 2 2 = U 1 + − 2 Z L Z C 2 + Z C 2 2 R 2 + Z L 2
Để U R không phụ thuộc vào R thì: − 2 Z L Z C 2 + Z C 2 2 = 0 ⇒ Z C 2 = 2 Z L 2
Từ (1) và (2) ta có: Z C 1 Z C 2 = C 2 C 1 = 1 2 ⇒ 2 C 2 = C 1