Chứng tỏ rằng: 1 101 + 1...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

10 tháng 3 2018

Chứng tỏ rằng:

1 101 + 1 102 + 1 102 + . . . + 1 200 > 1 2

#Toán lớp 6

Cao Minh Tâm

10 tháng 3 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

phạm quốc sang

12 tháng 3 2017 - olm

Chứng tỏ rằng \(\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+....+\frac{1}{200}>\frac{1}{2}\)

Chi tiết rõ ràng nha

#Toán lớp 6

Đinh Đức Hùng

12 tháng 3 2017

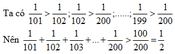
Ta có :

\(\frac{1}{101}>\frac{1}{200}\)

\(\frac{1}{102}>\frac{1}{200}\)

\(\frac{1}{103}>\frac{1}{200}\)

\(..........\)

\(\frac{1}{200}=\frac{1}{200}\)

Cộng vế với vế ta được :

\(\frac{1}{101}+\frac{1}{102}+....+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}\) (có 100 số \(\frac{1}{200}\) )\(=\frac{100}{200}=\frac{1}{2}\)

\(\Rightarrow\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+......+\frac{1}{200}>\frac{1}{2}\) (đpcm)

Đúng(0)

hoàng tuấn anh sơn

12 tháng 3 2017

Ta có:

1/101>1/200

1/102>1/200

...

1/199>1/200

=>1/101+1/102+...+1/103>1/200+1/200+...+1/200(100 số 1/200)

=1/200.100=1/2

Vậy 1/101+1/102+1/103+...+1/200>1/2

Đúng(0)

Huy Nguyễn

9 tháng 5 2019

Chứng tỏ rằng:\(\frac{1}{101}\)+\(\frac{1}{102}\)+\(\frac{1}{103}\)+......…...........+\(\frac{1}{200}\)

>\(\frac{1}{2}\)

#Toán lớp 6

Nguyễn Minh Thảo

10 tháng 5 2019

Ta có:

\(\frac{1}{101}\)>\(\frac{1}{200}\)

\(\frac{1}{102}\)>\(\frac{1}{200}\)

\(\frac{1}{103}\)>\(\frac{1}{200}\)

...

\(\frac{1}{200}\)=\(\frac{1}{200}\)

\(\frac{1}{101}\)+\(\frac{1}{102}\)+\(\frac{1}{103}\)+...+\(\frac{1}{200}\)>\(\frac{1}{200}\)+\(\frac{1}{200}\)+..+\(\frac{1}{200}\)(100 số hạng)=\(\frac{1}{2}\)

\(\Rightarrow\)\(\frac{1}{101}\)+\(\frac{1}{102}\)+\(\frac{1}{103}\)+...+\(\frac{1}{200}\)>\(\frac{1}{2}\)

Đúng(0)

Phạm Thị Thúy Kiều

7 tháng 5 2017 - olm

Chứng tỏ rằng : \(\frac{1}{101}\)+ \(\frac{1}{102}\)+ \(\frac{1}{103}\)+ .......+ \(\frac{1}{200}\)>\(\frac{1}{2}\)

#Toán lớp 6

Nguyễn Tiến Dũng

7 tháng 5 2017

1/2=1/200+1/200+1/200+.....+1/200 (có 100 số )

1/101+1/102+....+1/200(có 100 số )

Vì 1/101>1/200

1/102>1/100

......

1/199>1/200

1/200=1/200

=>1/101+1/102+.....+1/200>1/200+1/200+...+1/200 có 100 số

=>1/101+1/102+.....+1/200>1/2

Đúng(0)

Kaori Miyazono

7 tháng 5 2017

Ta thấy \(\frac{1}{101}>\frac{1}{200};\frac{1}{102}>\frac{1}{200};\frac{1}{103}>\frac{1}{200};....;\frac{1}{200}=\frac{1}{200}\)

Mà dãy \(\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+....+\frac{1}{200}\)có 100 phân số nên :

\(\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+...+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}\)( có 100 phân số \(\frac{1}{200}\))

\(\Rightarrow\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+...+\frac{1}{200}>\frac{1}{200}.100=\frac{1.}{2}\left(đpcm\right)\)

Đúng(0)

Nguyễn Mon

17 tháng 3 2016 - olm

Chứng tỏ rằng\(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{299}+\frac{1}{300}>\frac{2}{3}\)

#Toán lớp 6

Sách Giáo Khoa

15 tháng 5 2017

Chứng tỏ rằng :

\(\dfrac{1}{101}+\dfrac{1}{102}+.....+\dfrac{1}{299}+\dfrac{1}{300}>\dfrac{2}{3}\)

#Toán lớp 6

Hải Đăng

4 tháng 5 2018

Giáº£i sÃ¡ch bÃ i táºp ToÃ¡n 6 | Giáº£i bÃ i táºp SÃ¡ch bÃ i táºp ToÃ¡n 6

Đúng(0)

Võ Thiết Hải Đăng

5 tháng 5 2018

Giáº£i sÃ¡ch bÃ i táºp ToÃ¡n 6 | Giáº£i bÃ i táºp SÃ¡ch bÃ i táºp ToÃ¡n 6

Đúng(0)

Quang Ninh

15 tháng 3 2015 - olm

Chứng tỏ rằng \(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{299}+\frac{1}{300}>\frac{2}{3}\)

#Toán lớp 6

Anh Dao Tuan

15 tháng 3 2015

Đặt A=1/101+1/102+1/103+...+1/300

vì 1/101>1/102>1/103>...>1/300

=>(1/101+1/102+1/103+...+1/200)+(1/201+1/202+1/103+...+1/300) > (1/200+1/200+1/200+...+1/200)+(1/300+1/300+1/300+...+1/300) (mỗi ngoặc tên có tất cả là 100 phân số/1 ngoặc nhé!)

=>1/101+1/102+1/103+...+1/300 > (1/200).100 + (1/300).100

=> A > 1/2+1/3

=> A > 5/6

Mà 5/6>2/3

=> A > 2/3

Vậy 1/101+1/102+1/103+...+1/300 >2/3

Đúng(0)

văn Trường

31 tháng 3 2015

Vì : 1/101 > 1/300 ; 1/102 > 1/300 .... ; 1/299 >1/300 ; Do 1/101.....1/300 có 200 số

=>1/101+1/102+....+1/299+1/300 > 1/300 x 200

> 2/3

Đúng(0)

Lê Minh Tiểu Phượng

16 tháng 3 2018 - olm

Chứng minh rằng\(A = {1 \over 101}+{1\over 102} +{1\over 103}+{1\over 104}+...+{1\over 200}>{7\over 12}\)

#Toán lớp 6

Thế Đan Trần

11 tháng 6 2020 - olm

Chứng tỏ rằng:

\(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{199}+\frac{1}{200}< 1\)

Giúp mình ý!!!Mình cho like!!

#Toán lớp 6

๖²⁴ʱTú❄⁀ᶦᵈᵒᶫ

12 tháng 6 2020

Ta có : \(\frac{1}{101}>\frac{1}{200}\)

\(\frac{1}{102}>\frac{1}{200}\)

\(...>\frac{1}{200}\)

Mà \(\frac{1}{200}=\frac{1}{200}\)

Suy ra : \(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}\)

Mời nhân tài giải nốt.

Đúng(0)

Uyên

11 tháng 3 2018 - olm

\(\text{Chứng tỏ:}\)

\(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+.....+\frac{1}{199}-\frac{1}{200}=\frac{1}{101}+\frac{1}{102}+.....+\frac{1}{200}\)

#Toán lớp 6

11 tháng 3 2018

\(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{199}-\frac{1}{200}\)

\(=\left(1+\frac{1}{3}+...+\frac{1}{199}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{200}\right)\)

\(=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{200}-2\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{200}\right)\)

\(=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{200}-\left(1+\frac{1}{2}+...+\frac{1}{100}\right)\)

\(=\frac{1}{101}+\frac{1}{102}+...+\frac{1}{102}\) (đpcm)

Đúng(0)

Phan Thùy Dương

23 tháng 3 2017

Chứng tỏ rằng : \(\dfrac{1}{101}\) + \(\dfrac{1}{102}\) + ... + \(\dfrac{1}{299}\) + \(\dfrac{1}{300}\) > \(\dfrac{2}{3}\)

#Toán lớp 6

Nguyễn Ngọc Minh Châu

23 tháng 3 2017

Ta có:

\(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{299}+\dfrac{1}{300}>\dfrac{1}{300}.200=\dfrac{200}{300}=\dfrac{2}{3}\)

\(\Rightarrow\) biểu thức trên lớn hơn \(\dfrac{2}{3}\).

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP