Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4

Áp dụng BĐT cô si cho 3 số không âm x,y,z ta được:
\(x+y+z\ge3\sqrt[3]{xyz}\Rightarrow1\ge3\sqrt[3]{xyz}\Rightarrow xyz\le\frac{1}{27}\)
\(\left(x+y\right)+\left(y+z\right)+\left(z+x\right)\ge3\sqrt[3]{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)
=>2.(x+y+z) \(\ge3\sqrt[3]{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)
=>\(3\sqrt[3]{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\le2\Leftrightarrow\left(x+y\right)\left(y+z\right)\left(z+x\right)\le\frac{8}{27}\)
=>\(B\le\frac{1}{27}.\frac{8}{27}=\frac{8}{729}\)
Vậy GTLN của B là 8/729 hay k=8/729
=>93k=8



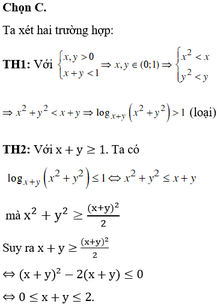
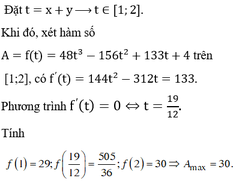
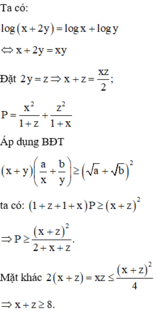
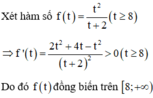
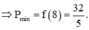
Từ đó
Sử dụng MTCT ta tìm được max P = 2 .
Chọn A.