Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

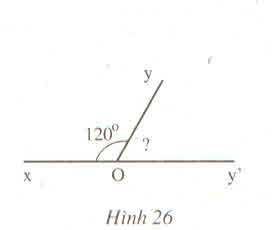
ta có : xOy va yOy' la hai goc ke nhau
=) xOy = 180 do
=> yOy' + xOy = xOy'
=> yOy' = xOy' - xOy =180 - 120 = 60 do
vay yOy' = 60 do

Ta có : xOy = 1/5 yOy
=> xOy/1 = yOy/5 = (xOy + yOy)/(1+5) = 180/6 = 30
=> xOy = 30 độ ; yOy = 150 độ
Sửa đề: cho 2 góc kề bù xOy và yOy'.Biết xOy = 1/5yOy' . Tính số đo các góc xOy và yOy'
y' x O y
Ta có:\(\widehat{xOy}=\frac{1}{5}\widehat{yOy}\Rightarrow\widehat{yOy}=\widehat{xOy}:\frac{1}{5}=5\widehat{xOy}\)
Mặt khác \(\widehat{xOy}+\widehat{yOy'}=180^0\)(kề bù)
\(\Rightarrow\widehat{xOy}+5\widehat{xOy}=180^0\)
\(\Rightarrow6\widehat{xOy}=180^0\)
\(\Rightarrow\widehat{xOy}=180^0:6=30^0\)
\(\Rightarrow\widehat{yOy'}=5.30^0=150^0\)


a. Vì \(\widehat{xOy}\)= 600
\(\widehat{yOz}\)=900
nên \(\widehat{xOy}\)< \(\widehat{yOz}\)(vì 60<90)
=> Tia oy nằm giữa 2 tia Ox và Oz
vì tia oy nằm giữa 2 tia Ox và Oz
nên \(\widehat{yOz}\)+ \(\widehat{xOy}\)= \(\widehat{xOz}\)
900 + 600 = \(\widehat{xOz}\)
\(\widehat{xOz}\) = 1500
b. Số đo của góc bù với góc xOy là 1200
k mk nha thư

Vì \(\widehat{xOy}\)và \(\widehat{yOz}\)là 2 góc kề bù nên có tổng số đo = \(^{180^o}\)
=> \(\widehat{yOz}\)= \(^{180^o-}\) \(\widehat{xOy}\)
= \(^{180^o-}\)\(^{70^o}\)
= \(^{110^0}\)
Vậy góc yOz = \(^{110^0}\)
Vì On là tia phân giác của góc xOy
=> yOn = \(\widehat{\frac{xOy}{2}}\)= \(\frac{^{180^o}}{2}\)= \(^{90^o}\)
Vậy yOn = \(^{90^o}\)
Vì góc yOn < góc yOz ( \(^{90^o< 110^o}\)) nên tia Oy nằm giữa On và Oz
=> nOz = yOn + yOz
= \(^{90^o+110^o}\)
= \(200^o\)

a) Trên nửa mp chứa tia Ox có \(\widehat{xOy}< \widehat{xOz}\)\(\left(60^0< 90^0\right)\)
Suy ra Oy nằm giữa \(\widehat{xOz}\)
Do đó \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
Hay \(60^0+\widehat{yOz}=90^0\)
\(\widehat{yOz}=90^0-60^0\)
\(\widehat{yOz}=30^0\)
b) Vì \(\widehat{yOx}\)và \(\widehat{xOy'}\)là hai góc kề bù
Do đó:\(\widehat{yOx}+\widehat{xOy'}=\widehat{yOy'}\)
\(60^0+\widehat{xOy'}=180^0\)
\(\widehat{xOy'}=180^0-60^0\)
\(\widehat{xOy'}=120^0\)
Đáp án là A
Vì ∠xOy và ∠yOy' là hai góc kề bù nên ta có: ∠xOy + ∠yOy' = 180 0 ⇒ ∠yOy' = 180 0 - 80 0 = 100 0