Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
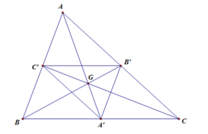
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C

Đáp án A
Ta có V G ; − 1 2 A = A ' ⇒ G A ' → = − 1 2 G A → ⇒ A ' là trung điểm của B ' C '
Tương tự, ta thấy B ' C ' lần lượt là trung điểm của A ' C ' , A ' B ' ⇒ S Δ A ' B ' C ' S Δ A B C = 1 4
Vậy tỉ số V S . A ' B ' C ' V S . A B C = d S ; A B C . S Δ A ' B ' C ' d S ; A B C . S Δ A B C = 1 4

Đáp án A
Do Δ A ' B ' C ' là ảnh của Δ A B C qua phép V G ; K = − 1 2
Do đó: S A ' B ' C ' S A B C = k 2 = 1 4 ⇒ V A ' B ' C ' V A B C = d S ; A B C . S A ' B ' C ' d S ; A B C . S A B C = 1 4

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
B A C M
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1/2 BC
Vì G là trọng tâm của ∆ ABC nên AG = 2/3 AM AM => AG = 2/3.1/2 BC
=> AG = 1/3 BC = 1/3.5 = 1.7cm

Đáp án A.
Gọi K(a;b) là tâm đường tròn ngoại tiếp Δ A B C .
Ta có: A K 2 = a - 1 2 + b - 2 2 ; B K 2 = a - 5 2 + b - 4 2 và
C K 2 = a - 3 2 + b + 2 2 .
Từ A K 2 = B K 2 = C K 2 , ta có a - 1 2 + b - 2 2 = a - 5 2 + b - 4 2 a - 1 2 + b - 2 2 = a - 3 2 + b + 2 2
⇔ - 2 a - 4 b + 5 = - 10 a - 8 b + 41 - 2 a - 4 b + 5 = - 6 a + 4 b + 13 ⇔ 2 a + b = 9 a - 2 b = 2 ⇔ a = 4 b = 1 → K 4 ; 1 .
Bán kính đường tròn ngoại tiếp ∆ A B C là R = A K = 4 - 1 2 + 1 - 2 2 = 10 .
Gọi K' là tâm đường tròn ngoại tiếp ∆ A ' B ' C ' , do V 1 ; - 3 = ∆ A B C = ∆ A ' B ' C ' nên V 1 ; - 3 K = K ' → I K → = - 3 I K → . Mà V 1 ; - 3 A = A ' → I A → = - 3 I A → .
Suy ra I A ' → - I K ' → = - 3 I A → - I K → ⇔ K ' A ' → = - 3 K A → . Bán kính đường tròn ngoại tiếp ∆ A ' B ' C ' là R = K ' A ' = 3 K A = 3 R = 3 10 .

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2
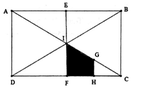
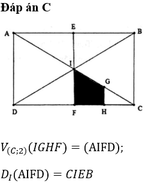

Đáp án B
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C