Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh tứ giác OBDF nội tiếp.
Định tâm I đường tròn ngoại tiếp tứ OBDF.
Ta có: DBO = 900 và DFO = 900(tính chất tiếp tuyến)
Tứ giác OBDF có DBO+DFO =1800 nên nội tiếp được trong một đường tròn.
Tâm I đường tròn ngoại tiếp tứ giác OBDF là trung điểm của OD
b) Tính Cos DAB .
Áp dụng định lí Pi-ta-go cho tam giác OFA vuông ở F ta được:
\(OA=\sqrt{OF^2+AF^2}=\sqrt{R^2+\left(\frac{4R}{3}\right)}=\frac{5R}{3}\)
\(COS\)\(FAO=\frac{AF}{OA}=\frac{4R}{3}:\frac{5R}{3}=0,8=>COSDAB=0,8\)
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh \(\frac{BD}{DM}-\frac{DM}{AM}\) =1
∗ OM // BD ( cùng vuông góc BC) ⇒ MOD BDO = (so le trong) và BDO ODM = (tính chất hai tiếp tuyến cắt nhau)
Suy ra: MDO =MOD.
Vậy tam giác MDO cân ở M. Do đó: MD = MO
∗ Áp dụng hệ quả định lí Ta let vào tam giác ABD có OM // BD ta được:
\(\frac{BD}{OM}=\frac{AD}{AM}HAY\frac{BD}{DM}=\frac{AD}{AM}\)(VÌ MD=MO)
\(=>\frac{BD}{DM}=\frac{AM+DM}{AM}=1+\frac{DM}{AM}\)
Do đó:\(\frac{DM}{BM}-\frac{DM}{AM}=1\left(đpcm\right)\)
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.
∗Áp dụng hệ thức lượng cho tam giác OAM vuông ở O có OF ⊥ AM ta được:
OF2 = MF. AF hay R2 = MF. \(\frac{4r}{3}\)⇒ MF = \(\frac{3r}{4}\)
∗ Áp dụng định lí pi ta go cho tam giác MFO vuông tại F ta được:
OM = \(\sqrt{OF^2+MF^2}=\sqrt{R^2+\frac{3R}{4}^2}=\frac{5R}{4}\)
∗ OM //BD =>\(\frac{OM}{BD}=\frac{AO}{AB}=>BD=\frac{OM.AB}{OA}=\frac{5R}{4}.\left(\frac{5R}{3}+R\right):\frac{5R}{3}=2R\)
Gọi S là diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O)
S1 là diện tích hình thang OBDM.
S2 là diện tích hình quạt góc ở tâm BON = 90 0
Ta có: S = S1 – S2 .
\(S1=\frac{1}{2}\left(OM+BD\right).OB=\frac{1}{2}\left(\frac{5R}{4}+2R\right).R=\frac{13R^2}{8}\left(đvdt\right)\)
\(S2=\frac{\pi R^2.90^0}{360^0}=\frac{\pi R^2}{4}\left(đvdt\right)\)
Vậys=s1-s2=\(\frac{13r^2}{8}-\frac{\pi r^2}{4}=\frac{r^2}{8}\left(13-2\pi\right)\left(đvdt\right)\)

a) Chứng minh tứ giác OBDF nội tiếp.
Xác định tâm I đường tròn ngoại tiếp tứ OBDF.
Giải :
Ta có: \(\widehat{DBO}=90^o\)và \(\widehat{DFO}=90^o\)(tính chất tiếp tuyến)
Tứ giác OBDF có \(\widehat{DBO}+\widehat{DFO}=90^o+90^o=180^o\)nên nội tiếp được trongmột đường tròn.
Tâm I đường tròn ngoại tiếp tứ giác OBDF là trung điểm của OD
mk làm được phần a rồi đấy, ai giúp mk phần b,c,d thôi. cảm ơn
tiện thể xem hộ xem đúng k nha

Lời giải:

a)
Vì $AF$ là tiếp tuyến của $(O)$ nên \(AF\perp OF\) hay \(DA\perp OF\Rightarrow \widehat{DFO}=90^0\)
$DB$ là tiếp tuyến của $(O)$ nên \(DB\perp OB\Rightarrow \widehat{DBO}=90^0\)
Tứ giác $DBOF$ có tổng hai góc đối nhau
\(\widehat{DFO}+\widehat{DBO}=90^0+90^0=180^0\) nên là tứ giác nội tiếp.
b)
Áp dụng định lý Pitago cho tam giác $OFA$ vuông tại $F$:
\(OA=\sqrt{OF^2+FA^2}=\sqrt{R^2+(\frac{4}{3}R)^2}=\frac{5}{3}R\)
Ta có:
\(\cos \widehat{DAB}=\cos \widehat{OAF}=\frac{FA}{OA}=\frac{\frac{4}{3}R}{\frac{5}{3}R}=\frac{4}{5}\)
c) \(OM\perp BA, BD\perp BA\Rightarrow OM\parallel BD\)
Theo tính chất hai đường tiếp tuyến cắt nhau suy ra $DO$ là phân giác góc \(\widehat{BDF}\)
\(\Rightarrow \widehat{BDO}=\widehat{ODM}\)
Mà \(OM\parallel BD\Rightarrow \widehat{MOD}=\widehat{ODB}\) (so le trong)
Suy ra \(\widehat{ODM}=\widehat{MOD}\Rightarrow \triangle MDO\) cân tại $M$
\(\Rightarrow MD=MO\)
Áp dụng định lý Thales với \(MO\parallel DB\) ta có:
\(\frac{DA}{MA}=\frac{DB}{MO}=\frac{DB}{DM}\)
\(\Leftrightarrow \frac{DM+MA}{MA}=\frac{DB}{DM}\Rightarrow \frac{BD}{DM}-\frac{DM}{AM}=1\) (đpcm)

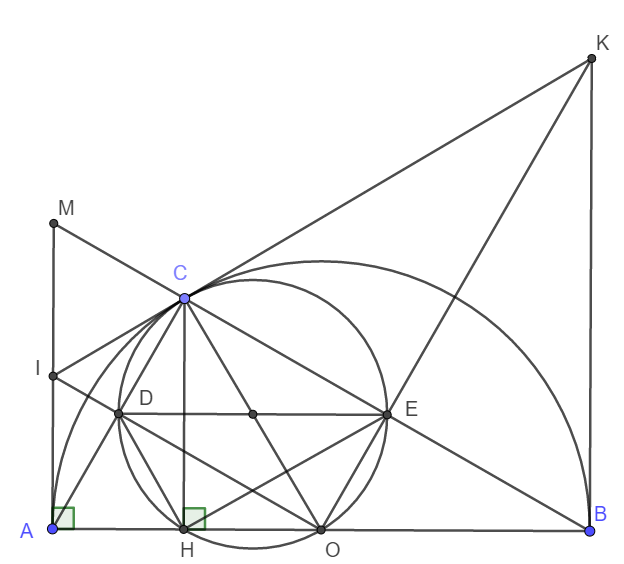
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.
 Phạm Cao Thúy An: Biết rồi còn hỏi làm gì?
Phạm Cao Thúy An: Biết rồi còn hỏi làm gì?
a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π